题目内容

（5x2+2x-3）2-（x2-2x-3）2=
 
．
考点：有理数指数幂的运算性质
专题：函数的性质及应用
分析：由条件平方差公式化简，提取公因式，可得答案．
解答： 解：（5x2+2x-3）2-（x2-2x-3）2=[（5x2+2x-3）+（x2-2x-3）]•[（5x2+2x-3）-（x2-2x-3）]
=（6x2-6）（4x2+4x）=24（x2-1）x（x+1）=24x（x+1）2（x-1），
故答案为：24x•（x2-1）•（x+1）
点评：本题主要考查平方差公式的应用，注意提取公因式，属于基础题．
练习册系列答案
相关题目
已知命题P：
x2
2m
+
y2
9-m
=1表示焦点在y轴上的椭圆，命题Q：双曲线
y2
5
-
x2
m
=1的离心率e∈（
6
2
，
2
），若命题P、Q中有且只有一个为真命题，求实数m的取值范围．
已知直角坐标系xoy中，直线的参数方程为
x=t-3
y=
3
t
（t为参数）．以直角坐标系xOy中的原点O为极点，x轴的非负半轴为极轴，圆C的极坐标方程为ρ2-6ρcosθ+5=0，则圆心C到直线距离为
 
．
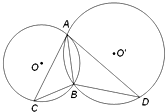如图，⊙O和⊙O′相交于A、B两点，过A作两圆的切线分别交两圆于C、D两点，连接DB、CB，已知BC=3，BD=4，则AB=
 
．
在极坐标系中，ρ=2θ+1（0≤θ＜2π）与θ=
π
2
的交点的极坐标为
 
．
已知数列{an}为：
1
1
，
2
1
，
1
2
，
3
1
，
2
2
，
1
3
，
4
1
，
3
2
，
2
3
，
1
4
，…，依它的前10项的规律，则a50=
 
．
数列{an}的前n项的和Sn=2n-1，则an=
 
．
在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，已知点A的极坐标为（
2
，
π
4
），直线l的极坐标方程为ρcos（θ-
π
4
）=a，且点A在直线l上，
（1）求a的值及直线l的直角坐标方程；
（2）圆C的参数方程为
x=1+cosα
y=sinα
（α为参数），试判断直线l与圆C的位置关系．
当0≤x≤
1
2
时，|ax-2x3|≤
1
2
恒成立，则实数a的取值范围是（　　）
A、
3
2
≥a≥-
1
2
B、-
1
2
≥a≥
1
2
C、a≥-
1
2
D、a≤
3
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网