题目内容
过P(2,0)作倾斜角为α的直线l与曲线E:
(θ为参数)交于A,B两点.
(Ⅰ)求曲线E的普通方程及l的参数方程;
(Ⅱ)求sinα的取值范围.
|
(Ⅰ)求曲线E的普通方程及l的参数方程;
(Ⅱ)求sinα的取值范围.
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(Ⅰ)利用同角三角函数的基本关系消去参数θ,可得曲线E的普通方程为 x2+2y2=1,由直线参数方程的特征可得L的参数方程为
(t为参数).
(Ⅱ)将L的参数方程代入由线E的方程得(1+sin2α)t2+(4cosα)t+3=0,由△≥0,得sin2α≤
,可得sinα的取值范围.
|
(Ⅱ)将L的参数方程代入由线E的方程得(1+sin2α)t2+(4cosα)t+3=0,由△≥0,得sin2α≤
| 1 |
| 7 |
解答:
解:(Ⅰ)消去参数θ,可得曲线E的普通方程为 x2+2y2=1,
由条件可得L的参数方程为
(t为参数).
(Ⅱ)将L的参数方程代入由线E的方程得(1+sin2α)t2+(4cosα)t+3=0,
由△=(4cosα)2-4(1+sin2α)×3≥0,得sin2α≤
.
又由于倾斜角α满足:0≤α<π,∴0≤sinα≤
.
由条件可得L的参数方程为
|
(Ⅱ)将L的参数方程代入由线E的方程得(1+sin2α)t2+(4cosα)t+3=0,
由△=(4cosα)2-4(1+sin2α)×3≥0,得sin2α≤
| 1 |
| 7 |
又由于倾斜角α满足:0≤α<π,∴0≤sinα≤
| ||
| 7 |
点评:本题考查把参数方程化为普通方程的方法,直线的参数方程,是一道基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
在△ABC中,a,b,c分别是内角A,B,C所对的边长,
=2
,
•
=0,
•
=-6,|
|=
.则内角B的大小为( )
| BD |
| DC |
| AB |
| AD |
| AB |
| BC |
| AD |
2
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
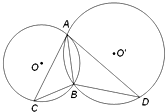 如图,⊙O和⊙O′相交于A、B两点,过A作两圆的切线分别交两圆于C、D两点,连接DB、CB,已知BC=3,BD=4,则AB=
如图,⊙O和⊙O′相交于A、B两点,过A作两圆的切线分别交两圆于C、D两点,连接DB、CB,已知BC=3,BD=4,则AB=