题目内容
给出命题:
(1)三棱锥的四个面都可以是直角三角形;
(2)有两个侧面都垂直于底面的四棱柱为直四棱柱;
(3)三棱锥中若有两组对棱互相垂直,则第三组对棱也一定互相垂直.
其中正确的命题是 (填正确的命题的序号)
(1)三棱锥的四个面都可以是直角三角形;
(2)有两个侧面都垂直于底面的四棱柱为直四棱柱;
(3)三棱锥中若有两组对棱互相垂直,则第三组对棱也一定互相垂直.
其中正确的命题是
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:(1)结合图形,令三棱锥A-BCD中AB⊥平面BCD,CD⊥平面ABC,可得(1)是正确的;
(2)根据若四棱柱的两个平行侧面都垂直于底面,其侧棱不一定与底面垂直,可得(2)是错误的;
(3)利用三垂线逆定理,可得S在底面的射影为底面三角形的垂心,再根据三垂线定理可得第三组对棱垂直.
(2)根据若四棱柱的两个平行侧面都垂直于底面,其侧棱不一定与底面垂直,可得(2)是错误的;
(3)利用三垂线逆定理,可得S在底面的射影为底面三角形的垂心,再根据三垂线定理可得第三组对棱垂直.
解答:
解:对(1)如图:

三棱锥A-BCD,其中AB⊥平面BCD,CD⊥平面ABC,则三棱锥的四个面都是直角三角形,故(1)正确;
对(2),若四棱柱的两个平行侧面都垂直于底面,其侧棱不一定与底面垂直,故(2)错误;
对(3),如图:

三棱锥,SO⊥平面ABC,∵SC⊥AB,SB⊥AC,∴O为△ABC的垂心,∴AO⊥BC,由三垂线定理得:SA⊥BC,故(3)正确.
故答案为:(1),(3).

三棱锥A-BCD,其中AB⊥平面BCD,CD⊥平面ABC,则三棱锥的四个面都是直角三角形,故(1)正确;
对(2),若四棱柱的两个平行侧面都垂直于底面,其侧棱不一定与底面垂直,故(2)错误;
对(3),如图:

三棱锥,SO⊥平面ABC,∵SC⊥AB,SB⊥AC,∴O为△ABC的垂心,∴AO⊥BC,由三垂线定理得:SA⊥BC,故(3)正确.
故答案为:(1),(3).
点评:本题考查了棱锥与棱柱的结构性质,熟练掌握棱锥的结构特征是解题的关键.

练习册系列答案
相关题目
若函数f(x)=x3-3x在(a,6-a2)上有最小值,则实数a的取值范围是( )
A、(-
| ||
B、[-
| ||
| C、[-2,1) | ||
| D、(-2,1) |
已知α是第四象限的角,并且cosα=
,那么tanα的值等于( )
| 4 |
| 5 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
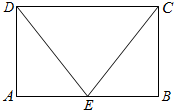 如图,矩形ABCD中,点E为边AB的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△AED或△BEC内部的概率等于( )
如图,矩形ABCD中,点E为边AB的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△AED或△BEC内部的概率等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
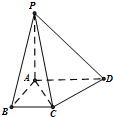 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,且PA=AD=2,AB=BC=1,则PD与平面PAC所成的角大小为
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,且PA=AD=2,AB=BC=1,则PD与平面PAC所成的角大小为