题目内容
不等式|2x+1|-|x-1|>2的解集为 .
考点:绝对值不等式的解法
专题:计算题,分类讨论,不等式的解法及应用
分析:通过对x分类讨论①当x>1时,②当-
≤x≤1时,③当x<-
时,去掉绝对值符号即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:①当x>1时,|2x+1|-|x-1|=2x+1-(x-1)=x+2,∴x+2>2,解得x>0,又x>1,∴x>1;
②当-
≤x≤1时,原不等式可化为2x+1+x-1>2,解得x>
,又-
≤x≤1,∴
<x≤1;
③当x<-
时,原不等式可化为-2x-1+x-1>2,解得x<-4,又x<-
,∴x<-4.
综上可知:原不等式的解集为(-∞,-4)∪(
,+∞).
故答案为:(-∞,-4)∪(
,+∞).
②当-
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
③当x<-
| 1 |
| 2 |
| 1 |
| 2 |
综上可知:原不等式的解集为(-∞,-4)∪(
| 2 |
| 3 |
故答案为:(-∞,-4)∪(
| 2 |
| 3 |
点评:本题考查绝对值不等式的解法,熟练掌握分类讨论思想方法是解含绝对值的不等式的常用方法之一.

练习册系列答案
相关题目
已知函数f(x)=log2(x2+1)的值域为{0,1,2},则满足这样条件的函数的个数为( )
| A、8 | B、5 | C、9 | D、27 |
已知函数f(x)=
在区间[1,3]上的最大值为A,最小值为B,则A+B=( )
| 2 |
| x |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
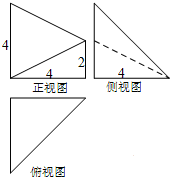 已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V=
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V=