题目内容
8.已知函数f(x)=(a+$\frac{1}{a}$)lnx-x+$\frac{1}{x}$,其中a>0.(Ⅰ)若f(x)在(0,+∞)上存在极值点,求a的取值范围;
(Ⅱ)设a∈(1,e],当x1∈(0,1),x2∈(1,+∞)时,记f(x2)-f(x1)的最大值为M(a),那么M(a)是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
分析 (Ⅰ)求出f′(x)=$\frac{-(x-a)(x-\frac{1}{a})}{{x}^{2}}$,x∈(0,+∞),由此根据a=1,a>0且a≠1,利用导数性质进行分类讨论,能求出a的取值范围.
(Ⅱ)当a∈(1,e]时,$\frac{1}{a}<1<a$,f(x)在(0,$\frac{1}{a}$)上单调递减,在($\frac{1}{a}$,a)上单调递增,在(a,+∞)上单调递减,对?x1∈(0,1),有f(x1)≥f($\frac{1}{a}$),对?x2∈(1,+∞),有f(x2)≤f(a),从而[f(x2)-f(x1)]max=f(a)-f($\frac{1}{a}$),由此能求出M(a)存在最大值$\frac{4}{e}$.
解答 解:(Ⅰ)∵f(x)=(a+$\frac{1}{a}$)lnx-x+$\frac{1}{x}$,其中a>0,
∴${f}^{'}(x)=(a+\frac{1}{a})\frac{1}{x}-1-\frac{1}{{x}^{2}}$=$\frac{-(x-a)(x-\frac{1}{a})}{{x}^{2}}$,x∈(0,+∞),
①当a=1时,${f}^{'}(x)=-\frac{(x-1)^{2}}{{x}^{2}}$≤0,
f(x)在(0,+∞)上单调递减,不存在极值点;
②当a>0时,且a≠1时,f′(a)=f′($\frac{1}{a}$)=0,
经检验a,$\frac{1}{a}$均为f(x)的极值点,
∴a∈(0,1)∪(1,+∞).
(Ⅱ)当a∈(1,e]时,$\frac{1}{a}<1<a$,
f(x)在(0,$\frac{1}{a}$)上单调递减,在($\frac{1}{a}$,a)上单调递增,
在(a,+∞)上单调递减,
对?x1∈(0,1),有f(x1)≥f($\frac{1}{a}$),对?x2∈(1,+∞),有f(x2)≤f(a),
∴[f(x2)-f(x1)]max=f(a)-f($\frac{1}{a}$),
∴M(a)=f(a)-f($\frac{1}{a}$)
=[(a+$\frac{1}{a}$)lna-a+$\frac{1}{a}$]-[(a+$\frac{1}{a}$)ln$\frac{1}{a}$-$\frac{1}{a}$+a]
=2[(a+$\frac{1}{a}$)lna-a+$\frac{1}{a}$],a∈(1,e],
M′(a)=2(1-$\frac{1}{{a}^{2}}$)lna+2(a+$\frac{1}{a}$)$\frac{1}{a}$+2(-1-$\frac{1}{{a}^{2}}$)
=2(1-$\frac{1}{{a}^{2}}$)lna,a∈(1,e].
∴M′(a)>0.即M(a)在(1,e]上单调递增,
∴[M(a)]max=M(e)=2(e+$\frac{1}{e}$)+2($\frac{1}{e}-e$)=$\frac{4}{e}$,
∴M(a)存在最大值$\frac{4}{e}$.
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.

| A. | $\frac{x^2}{8}-\frac{y^2}{24}=1$ | B. | $\frac{x^2}{24}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | D. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
 自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.
自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.(Ⅰ)求该企业2016年一年生产一件产品的利润的分布列和期望;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 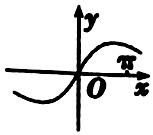 | B. |  | ||
| C. | 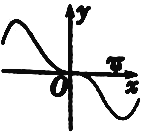 | D. | 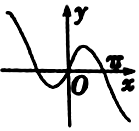 |
| A. | $[{-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6}}]$ | B. | $[{-\frac{1}{6},\frac{1}{6}}]$ | C. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | D. | $[{-\frac{1}{3},\frac{1}{3}}]$ |