题目内容

15．若二项式（x-$\frac{a}{x}$）6的展开式中常数项为20，则a=-1．

分析 利用通项公式即可得出．

解答 解：通项公式Tr+1=${∁}_{6}^{r}{x}^{6-r}（-\frac{a}{x}）^{r}$=（-a）r${∁}_{6}^{r}$x6-2r，令6-2r=0，解得r=3．
∴（-a）3${∁}_{6}^{3}$=20，解得a=-1．
故答案为：-1．

点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
5．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{1}{2}$，且过点$（1，\frac{3}{2}）$．若点M（x0，y0）在椭圆C上，则点$N（\frac{x_0}{a}，\frac{y_0}{b}）$称为点M的一个“椭点”．
（1）求椭圆C的标准方程；
（2）若直线l：y=kx+m与椭圆C相交于A，B两点，且A，B两点的“椭点”分别为P，Q，以PQ为直径的圆经过坐标原点，试求△AOB的面积．
6．已知函数f （x）=ex-ax-1，其中e为自然对数的底数，a∈R．
（1）若a=e，函数g （x）=（2-e）x．
①求函数h（x）=f （x）-g （x）的单调区间；
②若函数F（x）=$\left\{\begin{array}{l}f（x），x≤m\\ g（x），x＞m\end{array}$的值域为R，求实数m的取值范围；
（2）若存在实数x1，x2∈[0，2]，使得f（x1）=f（x2），且|x1-x2|≥1，求证：e-1≤a≤e2-e．
3．设$\frac{i}{1+i}$=a+bi（a，b∈R，i为虚数单位），则|a-bi|=（　　）
A．1B．$\frac{1}{2}$C．$\sqrt{2}$D．$\frac{\sqrt{2}}{2}$
10．等比数列{an}中，a3-3a2=2，且5a4为12a3和2a5的等差中项，则{an}的公比等于（　　）
A．3B．2或3C．2D．6
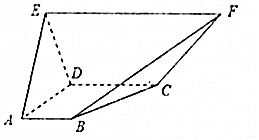20．在如图所示的五面体中，面ABCD为直角梯形，∠BAD=∠ADC=$\frac{π}{2}$，平面ADE⊥平面ABCD，EF=2DC=4AB=4，△ADE是边长为2的正三角形．
（Ⅰ）证明：BE⊥平面ACF；
（Ⅱ）求二面角A-BC-F的余弦值．
7．复数Z=i（1+i）在复平面内对应的点的坐标为（-1，1）．
4．已知等差数列{an}的前n项和为Sn，且满足S4=24，S7=63．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若bn=2an+an，求数列{bn}的前n项和Tn．
5．设函数$f（x）=\frac{1}{x}，g（x）=a{x^2}+bx（a，b∈R，a≠0）$，若y=f（x）的图象与y=g（x）图象有且仅有两个不同的公共点A（x1，y1），B（x2，y2），有如下命题：
①当a＜0时，x1+x2＜0，y1+y2＞0
②当a＜0时，x1+x2＞0，y1+y2＜0
③当a＞0时，x1+x2＜0，y1+y2＜0
④当a＞0时，x1+x2＞0，y1+y2＞0
其中，正确命题的序号是②．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网