题目内容
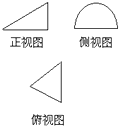 如图是某几何体的三视图,其中正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,则该几何体的体积是( )
如图是某几何体的三视图,其中正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,则该几何体的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知这是用轴截面分成两部分的半个圆锥,正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,得到圆锥是一个底面半径是a,母线长是2a,利用圆锥的体积公式得到结果.
解答:
解:由三视图可知这是用轴截面分成两部分的半个圆锥,
∵正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,
∴圆锥是一个底面半径是a,母线长是2a,
∴圆锥的高是
=
a,
∴半个圆锥的体积是
×
×π×a2×
a=
πa3,
故选C.
∵正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,
∴圆锥是一个底面半径是a,母线长是2a,
∴圆锥的高是
| (2a)2-a2 |
| 3 |
∴半个圆锥的体积是
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| ||
| 6 |
故选C.
点评:本题考查由三视图得到直观图,考查求简单几何体的体积,本题不是一个完整的圆锥,只是圆锥的一部分,这样不好看出直观图.

练习册系列答案
相关题目
非空数集A={a1,a2,a3,…,an}(n∈N*)中,所有元素的算术平均数记为E(A),即E(A)=
.若非空数集B满足下列两个条件:①B⊆A;②E(B)=E(A).则称B是A的一个“保均值子集”.据此,集合{2,3,4,5,6}的“保均值子集”有( )
| a1+a2+a3+…+an |
| n |
| A、5个 | B、6个 | C、7个 | D、8个 |
若f(x)=x2+(4cosθ)x-1在[1,
]上为增函数,则θ的取值范围是( )
| 3 |
A、[2kπ-
| ||||
B、[2kπ-
| ||||
C、[2kπ+
| ||||
D、[2kπ-
|
甲、乙、丙、丁四个人排成一行,则乙、丙相邻的排法种数是( )
| A、6 | B、8 | C、12 | D、24 |
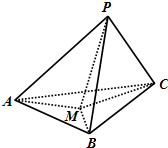 如图,在三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=3,PB=2,PC=1,设M是底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积,若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=3,PB=2,PC=1,设M是底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积,若f(M)=(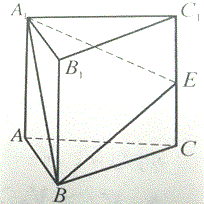 正三棱柱ABC-A1B1C1中,所有棱长都是4,E是CC1的中点.
正三棱柱ABC-A1B1C1中,所有棱长都是4,E是CC1的中点.