题目内容
 已知二面角α-AB-β的平面角为600,直线OP在平面α内,∠POA=60°,直线m为
已知二面角α-AB-β的平面角为600,直线OP在平面α内,∠POA=60°,直线m为平面β内的任意一条直线,则直线OP与直线m所成角正弦的最小值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离
分析:过P做PC⊥β,垂足为C,作CD⊥AB,垂足为D,连接PD,则∠PDC=60°,∠POD=60°,∠POC是直线OP与平面β的所成的角.根据最小角定理:直线与平面所成角是直线与平面内所有直线成角中最小的角,即可得出结论.
解答:
 解:如图所示,过P做PC⊥β,垂足为C,作CD⊥AB,垂足为D,连接PD,则∠PDC=60°,∠POD=60°,∠POC是直线OP与平面β的所成的角.
解:如图所示,过P做PC⊥β,垂足为C,作CD⊥AB,垂足为D,连接PD,则∠PDC=60°,∠POD=60°,∠POC是直线OP与平面β的所成的角.
设PD=2,则PO=
,PC=
,
∴sin∠POC=
=
.
根据最小角定理:直线与平面所成角是直线与平面内所有直线成角中最小的角,
则直线OP与直线m所成角正弦的最小值为
,
故选:A.
 解:如图所示,过P做PC⊥β,垂足为C,作CD⊥AB,垂足为D,连接PD,则∠PDC=60°,∠POD=60°,∠POC是直线OP与平面β的所成的角.
解:如图所示,过P做PC⊥β,垂足为C,作CD⊥AB,垂足为D,连接PD,则∠PDC=60°,∠POD=60°,∠POC是直线OP与平面β的所成的角.设PD=2,则PO=
| 4 | ||
|
| 3 |
∴sin∠POC=
| PC |
| PO |
| 3 |
| 4 |
根据最小角定理:直线与平面所成角是直线与平面内所有直线成角中最小的角,
则直线OP与直线m所成角正弦的最小值为
| 3 |
| 4 |
故选:A.
点评:本题考查与二面角有关的立体几何综合题,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
阅读如图所示的程序框图,若输入的n=10,则该算法的功能是( )
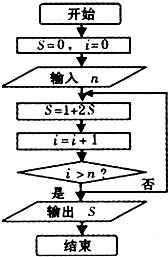

| A、计算数列{2n-1}的前11项和 |
| B、计算数列{2n-1}的前10项和 |
| C、计算数列{2n-1}的前11项和 |
| D、计算数列{2n-1}的前10项和 |
《中国好歌曲》的五位评委刘欢、杨坤、周华健、蔡健雅、羽•泉组合给一位歌手给出的评分分别是:x1=18,x2=19,x3=20,x4=21,x5=22,现将这五个数据依次输入下面程序框进行计算,则输出的S值及其统计意义分别是( )


| A、S=2,即5个数据的方差为2 |
| B、S=2,即5个数据的标准差为2 |
| C、S=10,即5个数据的方差为10 |
| D、S=10,即5个数据的标准差为10 |
如果复数
(其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于( )
| 2-bi |
| 1+2i |
| A、-6 | ||
B、
| ||
C、-
| ||
| D、2 |
某几何体的三视图如图所示,则该几何体的体积为( )
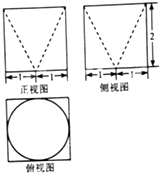

A、
| ||
B、
| ||
C、8-
| ||
D、8-
|
设m,n是正整数,多项式(1-2x)m+(1-5x)n中含x一次项的系数为-16,则含x2项的系数是( )
| A、-13 | B、6 | C、79 | D、37 |