题目内容
已知数列{an}的首项为1,数列{bn}为等比数列,且bn=
,若b1b20=2,则a21= .
| an+1 |
| an |
考点:等比数列的性质
专题:等差数列与等比数列
分析:根据bn=
和数列{an}的首项为1,把数列{an}的项用数列{bn}中的项表示,利用归纳推理和等比数列的性质求解.
| an+1 |
| an |
解答:
解:由题意知,bn=
,数列{an}的首项为1,
所以b1=
,则a2=b1,
b2=
,a3=a2b2=b1b2,
b3=
,a4=a3b3=b1b2b3,
…
得到:an=b1b2…bn-1,所以a21=b1b2…b20,
∵数列{bn}为等比数列,b1b20=2,
∴a21=(b1b20)(b2b19)…(b10b11)=(b1b20)10=210=1024,
故答案为:1024.
| an+1 |
| an |
所以b1=
| a2 |
| a1 |
b2=
| a3 |
| a2 |
b3=
| a4 |
| a3 |
…
得到:an=b1b2…bn-1,所以a21=b1b2…b20,
∵数列{bn}为等比数列,b1b20=2,
∴a21=(b1b20)(b2b19)…(b10b11)=(b1b20)10=210=1024,
故答案为:1024.
点评:本题考查了等比数列的性质,归纳推理,考查了数学转化思想方法,解答的关键是把数列{an}的项用数列{bn}中的项表示,是中档题.

练习册系列答案
相关题目
已知函数f(x)=
,g(x)=asin(
x)-2a+2(a>0,x∈[0,1]).若a∈[
,1].则( )
|
| π |
| 6 |
| 1 |
| 2 |
| A、?x1,x2∈[0,1],f(x1)=g(x2) |
| B、?x1∈[0,1],?x2∈[0,1],f(x1)=g(x2) |
| C、?x1,x2∈[0,1],f(x1)≥g(x2) |
| D、?x1∈[0,1],?x2∈[0,1],f(x1)≥g(x2) |
若对?x1∈(0,2],?x2∈[1,2],使4x1lnx1-x12+3+4x1x22+8ax1x2-16x1≥0成立,则a的取值范围是( )
A、[-
| ||||
B、[
| ||||
C、[-
| ||||
D、[-∞,
|
已知集合A={1,m2+1},B={2,4},则“m=
”是“A∩B={4}”的( )
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
某几何体的三视图如图所示,则该几何体的体积为( )
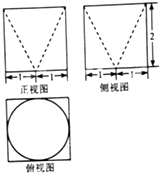

A、
| ||
B、
| ||
C、8-
| ||
D、8-
|