题目内容
13.若a=($\frac{1}{2}$)${\;}^{\frac{1}{5}}$,b=($\frac{1}{5}$)${\;}^{-\frac{1}{2}}$,c=log${\;}_{\frac{1}{5}}$10,则a,b,c大小关系为( )| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:a=($\frac{1}{2}$)${\;}^{\frac{1}{5}}$∈(0,1),b=($\frac{1}{5}$)${\;}^{-\frac{1}{2}}$>1,c=log${\;}_{\frac{1}{5}}$10<0,
∴b>a>c.
故选:B.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
8.已知抛物线C:y2=2px(p>0)和动直线l:y=kx+b(k,b是参变量,且k≠0.b≠0)相交于A(x1,y2),N)x2,y2)两点,直角坐标系原点为O,记直线OA,OB的斜率分别为kOA•kOB=$\sqrt{3}$恒成立,则当k变化时直线l恒经过的定点为( )
| A. | (-$\sqrt{3}$p,0) | B. | (-2$\sqrt{3}$p,0) | C. | (-$\frac{\sqrt{3}p}{3}$,0) | D. | (-$\frac{2\sqrt{3}p}{3}$,0) |
3.下列说法错误的是( )
| A. | 回归直线过样本点的中心($\overline{x}$,$\overline{y}$) | |
| B. | 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1 | |
| C. | 对分类变量X与Y,随机变量K2的观测值越大,则判断“X与Y有关系”的把握程度越小 | |
| D. | 在回归直线方程$\stackrel{∧}{y}$=0.2x+0.8中,当解释变量x每增加1个单位时预报变量$\stackrel{∧}{y}$平均增加0.2个单位 |
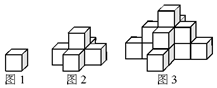 图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第六个叠放的图形中,小正方体木块总数就是( )
图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第六个叠放的图形中,小正方体木块总数就是( )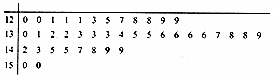 在高三某次数学测试中,40名优秀学生的成绩如图所示:
在高三某次数学测试中,40名优秀学生的成绩如图所示: