题目内容
若点(a,4)到直线x-2y+2=0的距离是2
,且在不等式3x+y-3>0表示的平面区域内,则a= .
| 5 |
考点:点到直线的距离公式
专题:直线与圆
分析:由距离公式可得a的方程,解得a值验证可得.
解答:
解:∵点(a,4)到直线x-2y+2=0的距离是2
,
∴由点到直线的距离公式可得
=2
,
解得a=16或a=-4,
经检验当a=16时,不等式3x+y-3>0成立,
当a=-4时,不等式3x+y-3>0不成立,
∴a=16
故答案为:16
| 5 |
∴由点到直线的距离公式可得
| |a-2×4+2| | ||
|
| 5 |
解得a=16或a=-4,
经检验当a=16时,不等式3x+y-3>0成立,
当a=-4时,不等式3x+y-3>0不成立,
∴a=16
故答案为:16
点评:本题考查点到直线的距离公式,涉及不等式与平面区域的关系,属基础题.

练习册系列答案
相关题目
设1<x<2,则
、(
)2、
的大小关系是( )
| lnx |
| x |
| lnx |
| x |
| lnx2 |
| x2 |
A、(
| ||||||
B、
| ||||||
C、(
| ||||||
D、
|
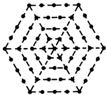 如图,有一个形如六边形的点阵,它的中心是一个点(算第1层),第2层每边有两个点,第3层每边有三个点,依此类推.
如图,有一个形如六边形的点阵,它的中心是一个点(算第1层),第2层每边有两个点,第3层每边有三个点,依此类推.