题目内容
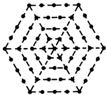 如图,有一个形如六边形的点阵,它的中心是一个点(算第1层),第2层每边有两个点,第3层每边有三个点,依此类推.
如图,有一个形如六边形的点阵,它的中心是一个点(算第1层),第2层每边有两个点,第3层每边有三个点,依此类推.(1)试问第n层(n∈N*且n≥2)的点数为
(2)如果一个六边形点阵共有169个点,那么它一共有
考点:归纳推理
专题:常规题型,推理和证明
分析:本题属于归纳推理题,(1)先对第2层、第三层、第四层等的点数进行统计,再归纳出一般性规律;(2)用归纳出的结论解决问题.
解答:
解:(1)由于形如六边形的点阵,它的中心是一个点(算第1层),
第2层每边有两个点,共有6条边,点数为6×2个,减去重复的6个顶点,得到(6×2-6)个,
第3层每边有三个点,共有6条边,点数为6×3个,减去重复的6个顶点,得到(6×3-6)个,
第4层每边有四个点,共有6条边,点数为6×4个,减去重复的6个顶点,得到(6×4-6)个,
…
归纳猜想得:
第n层每边有n个点,共有6条边,点数为6n个,减去重复的6个顶点,得到(6n-6)个.
(2)由(1)知:1+6+12+18+…+(6n-6)=169,
∴1+
×(n-1)=169,
∴n=8.
故答案为:(1)6(n-1); (2)8.
第2层每边有两个点,共有6条边,点数为6×2个,减去重复的6个顶点,得到(6×2-6)个,
第3层每边有三个点,共有6条边,点数为6×3个,减去重复的6个顶点,得到(6×3-6)个,
第4层每边有四个点,共有6条边,点数为6×4个,减去重复的6个顶点,得到(6×4-6)个,
…
归纳猜想得:
第n层每边有n个点,共有6条边,点数为6n个,减去重复的6个顶点,得到(6n-6)个.
(2)由(1)知:1+6+12+18+…+(6n-6)=169,
∴1+
| 6+(6n-6) |
| 2 |
∴n=8.
故答案为:(1)6(n-1); (2)8.
点评:本题考查的是归纳推理,难点在于找到各层点的个数的规律,本题还可以从项点数6出发,加上各边上的点的个数(n-2),(n≥2)得到6+6(n-2)去计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)是定义在R上的可导函数,其导函数记为f′(x),若对于任意实数x,有f(x)>f′(x),且y=f(x)-1为奇函数,则不等式f(x)<ex的解集为( )
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,e4) |
| D、(e4,+∞) |