题目内容
已知曲线C1:
(θ为参数),直线C2:
(t为参数),在曲线C1求一点,使它到直线C2的距离最小,并求出该点的直角坐标和最小距离.
|
|
考点:圆的参数方程
专题:坐标系和参数方程
分析:首先,将给定的曲线化为相应的普通方程,然后,判断直线与圆的位置关系,最后,确定最小值及取得最小值时点的坐标.
解答:
解:由曲线C1:
(θ为参数),
得 (x-1)2+y2=1,
直线C2:
(t为参数),
得x+y+2
-1=0.
∵圆心(1,0)到直线的距离d=
=2>r=1,
∴直线与圆相离,
故最大值为d+r=2+1=3,
最小值为d-r=2-1=1,
此时,当取得最小值时,直线方程为:x-y-1=0,
联立
,
解得
或
,
结合题意,得取(1-
,-
)时,取得最小值1.
|
得 (x-1)2+y2=1,
直线C2:
|
得x+y+2
| 2 |
∵圆心(1,0)到直线的距离d=
|1+0+2
| ||
|
∴直线与圆相离,
故最大值为d+r=2+1=3,
最小值为d-r=2-1=1,
此时,当取得最小值时,直线方程为:x-y-1=0,
联立
|
解得
|
|
结合题意,得取(1-
| ||
| 2 |
| ||
| 2 |
点评:本题重点考查了直线的参数方程和圆的参数方程、直线与圆的位置关系、最值问题的处理思路和方法等知识,属于中档题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是( )


| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
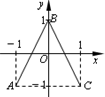 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )