题目内容
11.若-$\frac{π}{2}$<α<0,则直线y=-xcotα+1的倾斜角为( )| A. | -α | B. | α+$\frac{π}{2}$ | C. | α+π | D. | $\frac{π}{2}$-α |
分析 利用直线的倾斜角与斜率的关系、诱导公式即可得出.
解答 解:设直线y=-xcotα+1的倾斜角为θ,θ∈[0,π).
则tanθ=-cotα=-$\frac{cosα}{sinα}$=$\frac{sin(\frac{π}{2}+α)}{cos(\frac{π}{2}+α)}$=tan$(\frac{π}{2}+α)$,
∵-$\frac{π}{2}$<α<0,∴$0<\frac{π}{2}+α<\frac{π}{2}$.
∴θ=$\frac{π}{2}+α$.
故选:B.
点评 本题考查了直线的倾斜角与斜率的关系、诱导公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
2.已知集合A={x∈R||x-1|<1},B={y∈R|y=2x+1,x∈R},则A∩(∁RB)=( )
| A. | (0,2) | B. | [1,2) | C. | (0,1] | D. | (0,1) |
3.函数y=sin(2x+$\frac{π}{6}$)的图象可看成是把函数y=sin2x的图象做以下平移得到( )
| A. | 向右平移$\frac{π}{6}$ | B. | 向左平移 $\frac{π}{12}$ | C. | 向右平移 $\frac{π}{12}$ | D. | 向左平移$\frac{π}{6}$ |
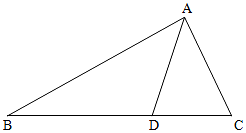 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$.