题目内容
1.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点P(1,$\frac{3}{2}$),且一个焦点为F1(-1,0).(1)求椭圆E的方程;
(2)若PA、PB、PC为椭圆E的三条弦,PA、PB所在的直线分别与x轴交于点M,N,且|PM|=|PN|,PC∥AB,求直线PC的方程.
分析 (1)由椭圆过点P(1,$\frac{3}{2}$),且一个焦点为F1(-1,0),列出方程组,求出a=2,b=$\sqrt{3}$,由此能求出椭圆E的方程.
(2)设PA:y=k(x-1)+$\frac{3}{2}$,A(xA,yA),B(xB,yB),联立$\left\{\begin{array}{l}{y=k(x-1)+\frac{3}{2}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2+4k(-2k+3)x+4k2-12k-3=0,由此利用韦过定理,求出${x}_{A}=\frac{4{k}^{2}-12k-3}{3+4{k}^{2}}$,yA=$\frac{-12{k}^{2}-6k}{3+4{k}^{2}}+\frac{3}{2}$,用-k代替k,得${x}_{B}=\frac{4{k}^{2}+12k-3}{3+4{k}^{2}}$,${y}_{B}=\frac{-12{k}^{2}+6k}{3+4{k}^{2}}+\frac{3}{2}$,从而得到kAB=$\frac{1}{2}$,再由PC∥AB,能求出直线PC的方程.
解答 解:(1)∵椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点P(1,$\frac{3}{2}$),且一个焦点为F1(-1,0),
∴$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{\frac{9}{4}}{{b}^{2}}=1}\\{c=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,又a>b>0,解得a=2,b=$\sqrt{3}$,
∴椭圆E的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)由题意知直线PA的斜率存在,
设PA:y=k(x-1)+$\frac{3}{2}$,A(xA,yA),B(xB,yB),
联立$\left\{\begin{array}{l}{y=k(x-1)+\frac{3}{2}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2+4k(-2k+3)x+4k2-12k-3=0,
∴${x}_{P}•{x}_{A}=1×{x}_{A}=\frac{4{k}^{2}-12k-3}{3+4{k}^{2}}$,
∴${x}_{A}=\frac{4{k}^{2}-12k-3}{3+4{k}^{2}}$,${y}_{A}=k({x}_{A}-1)+\frac{3}{2}$=$\frac{-12{k}^{2}-6k}{3+4{k}^{2}}+\frac{3}{2}$,
∵|PM|=|PN|,∴直线PB的斜率为-k,
用-k代替k,得${x}_{B}=\frac{4{k}^{2}+12k-3}{3+4{k}^{2}}$,${y}_{B}=\frac{-12{k}^{2}+6k}{3+4{k}^{2}}+\frac{3}{2}$,
${k}_{AB}=\frac{{y}_{A}-{y}_{B}}{{x}_{A}-{x}_{B}}$=$\frac{\frac{-12{k}^{2}+6k}{3+4{k}^{2}}+\frac{3}{2}-\frac{-12{k}^{2}-6k}{3+4{k}^{2}}-\frac{3}{2}}{\frac{4{k}^{2}+12k-3}{3+4{k}^{2}}-\frac{4{k}^{2}-12k-3}{3+4{k}^{2}}}$=$\frac{1}{2}$,
又∵PC∥AB,∴直线PC的方程为y-$\frac{3}{2}=\frac{1}{2}$(x-1),即x-2y+2=0.
点评 本题考查椭圆方程的求法,考查直线方程的求法,是中档题,解题时要认真审题,注意椭圆、直线方程、韦达定理等知识点的合理运用.

 名校课堂系列答案
名校课堂系列答案| A. | -α | B. | α+$\frac{π}{2}$ | C. | α+π | D. | $\frac{π}{2}$-α |
| A. | (0.1,0.2,0.3) | B. | (0,0,0.001) | C. | (5,0,0) | D. | (0,0.01,0) |
| A. | 1 | B. | 28 | C. | 212 | D. | 215 |
| A. | 1+i | B. | 1-i | C. | $\frac{{\sqrt{2}}}{2}-\frac{{\sqrt{2}}}{2}i$ | D. | $\frac{{\sqrt{2}}}{2}+\frac{{\sqrt{2}}}{2}i$ |
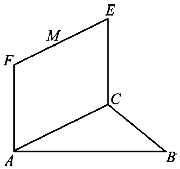 如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.
如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.