题目内容
1.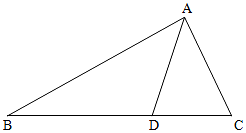 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$.(Ⅰ)求sin∠C的值;
(Ⅱ)若BD=2DC,求边AB的长.
分析 (Ⅰ)由平方关系求出sin∠ADB的值,由图象和两角差的正弦公式求出sinC的值;
(Ⅱ)由(I)和正弦定理求出CD的长,利用余弦定理求出边AB的长.
解答 解:(Ⅰ)在△ABC中,因为cos∠ADB=-$\frac{\sqrt{2}}{10}$且∠ADB∈(0,π),(1分)
所以sin∠ADB=$\frac{7\sqrt{2}}{10}$.(2分)
因为∠CAD=$\frac{π}{4}$,所以C=∠ADB-$\frac{π}{4}$.(3分)
所以sin∠C=sin(∠ADB-$\frac{π}{4}$)=$\frac{7\sqrt{2}}{10}×\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{10}×\frac{\sqrt{2}}{2}$=$\frac{4}{5}$.(6分)
(Ⅱ)在△ACD中,由正弦定理得$\frac{\frac{7}{2}}{\frac{7\sqrt{2}}{10}}=\frac{CD}{\frac{\sqrt{2}}{2}}$,∴CD=$\frac{5}{2}$,
∵BD=2DC,∴BC=$\frac{15}{2}$,
∴AB=$\sqrt{\frac{49}{4}+\frac{225}{4}-2×\frac{7}{2}×\frac{15}{2}×\frac{3}{5}}$=$\sqrt{37}$.
点评 本题考查正弦定理、余弦定理,两角差的正弦公式,考查化简、计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.若-$\frac{π}{2}$<α<0,则直线y=-xcotα+1的倾斜角为( )
| A. | -α | B. | α+$\frac{π}{2}$ | C. | α+π | D. | $\frac{π}{2}$-α |
 在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,Q是棱CC1上的动点,则当BQ+D1Q的长度取得最小值时,直线B1Q和直线BD所成的角的正切值是$\frac{\sqrt{5}}{2}$.
在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,Q是棱CC1上的动点,则当BQ+D1Q的长度取得最小值时,直线B1Q和直线BD所成的角的正切值是$\frac{\sqrt{5}}{2}$.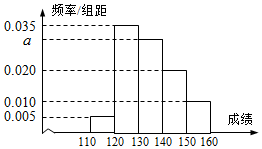 从高三年级随机抽取200名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为60.
从高三年级随机抽取200名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为60.