题目内容
20.已知复数z满足z=(2-i)(1+2i),其中i为虚数单位,则|z|=5.分析 利用复数的运算法则、模的计算公式即可得出.
解答 解:z=(2-i)(1+2i)=4+3i,则|z|=$\sqrt{{4}^{2}+{3}^{2}}$=5.
故答案为:5.
点评 本题考查了复数的运算法则、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
11.若-$\frac{π}{2}$<α<0,则直线y=-xcotα+1的倾斜角为( )
| A. | -α | B. | α+$\frac{π}{2}$ | C. | α+π | D. | $\frac{π}{2}$-α |
8.一本新出版的数学活动课教材在某书店销售,按事先拟定的价格进行5天试销,每种进价试销1天,得到如下数据:
(Ⅰ)若y与x线性相关,且回归直线方程为y=mx+132,求实数m的值;
(Ⅱ)预计以后的销售中,销量与单价服从(Ⅰ)中的回归直线方程,若每本数学活动课教材的成本是14元,为了获得最大利润,该教材的单价应为多少元?
| 单价x(元) | 18 | 19 | 20 | 21 | 22 |
| 销量y(册) | 61 | 56 | 50 | 48 | 45 |
(Ⅱ)预计以后的销售中,销量与单价服从(Ⅰ)中的回归直线方程,若每本数学活动课教材的成本是14元,为了获得最大利润,该教材的单价应为多少元?
15.集合A={x|x2-a≤0},B={x|x<2},若A⊆B,则实数a的取值范围是( )
| A. | (-∞,4] | B. | (-∞,4) | C. | [0,4] | D. | (0,4) |
5.已知点P是△ABC的中位线EF上任意一点,且EF∥BC,实数x,y满足$\overrightarrow{PA}+x\overrightarrow{PB}+y\overrightarrow{PC}=\overrightarrow 0$,设△ABC,△PBC,△PCA,△PAB的面积分别为S,S1,S2,S3,记$\frac{S_1}{S}={λ_1}$,$\frac{S_2}{S}={λ_2}$,$\frac{S_3}{S}={λ_3}$,则λ2•λ3取最大值时,3x+y的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
12.空间直角坐标系中,下列点在x 轴上的是( )
| A. | (0.1,0.2,0.3) | B. | (0,0,0.001) | C. | (5,0,0) | D. | (0,0.01,0) |
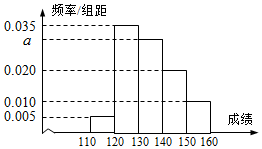 从高三年级随机抽取200名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为60.
从高三年级随机抽取200名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为60.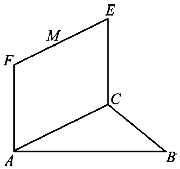 如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.
如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.