题目内容
17.已知数列{an}的前n项和为Sn,a1=1,当n≥2时,2Sn=(n+1)an-2.(Ⅰ)求a2,a3和通项an;
(Ⅱ)设数列{bn}满足bn=an•2n-1,求{bn}的前n项和Tn.
分析 (I)a1=1,当n≥2时,2Sn=(n+1)an-2.可得2(1+a2)=3a2-2,解得a2,a3.当n≥3时,2an=2(Sn-Sn-1),化为:$\frac{{a}_{n}}{n}=\frac{{a}_{n-1}}{n-1}$.即可得出.
(Ⅱ)由(I)可知,bn=an•2n-1,bn=$\left\{\begin{array}{l}{1,n=1}\\{n•{2}^{n},n≥2}\end{array}\right.$.即可得出.
解答 解:(I)a1=1,当n≥2时,2Sn=(n+1)an-2.∴2(1+a2)=3a2-2,解得a2=4.
同理可得:a3=6.当n≥3时,2an=2(Sn-Sn-1)=(n+1)an-2-(nan-1-2),化为:$\frac{{a}_{n}}{n}=\frac{{a}_{n-1}}{n-1}$.
∵$\frac{{a}_{3}}{3}=\frac{{a}_{2}}{2}$=2,a1=1,∴$\frac{{a}_{n}}{n}=\frac{{a}_{n-1}}{n-1}$=…=$\frac{{a}_{2}}{2}$=2.
∴n≥2时,an=2n.故an=$\left\{\begin{array}{l}{1,n=1}\\{2n,n≥2}\end{array}\right.$.
(Ⅱ)由(I)可知,bn=an•2n-1,bn=$\left\{\begin{array}{l}{1,n=1}\\{n•{2}^{n},n≥2}\end{array}\right.$.
所以当n=1时,Tn=b1=1.
当n≥2时,Tn=b1+b2+…+bn=1+2×22+3×23+…+n•2n,
则2Tn=2+2×23+…+(n-1)•2n+n•2n+1,
作差得:-Tn=1+2+(22+23+24+…+2n)-n•2n+1=1+$\frac{2({2}^{n}-1)}{2-1}$-n•2n+1=(1-n)•2n+1-1,
∴Tn=(n-1)•2n+1+1,n∈N*.(n=1时也成立).
点评 本题考查了等比数列的通项公式与求和公式、“错位相减法”方法、数列递推关系,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (-2,3] | B. | [-2,3] | C. | [-2,2] | D. | (-∞,-2]∪[3,+∞) |
| A. | $\frac{{x}^{2}}{15}$+$\frac{{y}^{2}}{14}$=1 | B. | $\frac{{x}^{2}}{17}$+$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{15}$=1 | D. | $\frac{{x}^{2}}{14}$+$\frac{{y}^{2}}{13}$=1 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | p∨q | B. | p∧q | C. | ¬p∧q | D. | p∨¬q |
| A. | $\sqrt{2}$ | B. | 2i | C. | $-\sqrt{2}$ | D. | .2+2i |
| A. | {0,1} | B. | {-1,0} | C. | {-1,0,1} | D. | {0,1,2} |

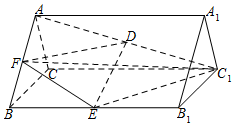 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分别为AC1和BB1的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分别为AC1和BB1的中点.