题目内容
2.i是虚数单位.已知复数$Z=\frac{1+3i}{3+i}+{({1+i})}^2$,则复数Z对应点落在( )| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
分析 利用复数的除法运算法则以及多项式乘法运算法则化简求解即可.
解答 解:复数$Z=\frac{1+3i}{3+i}+{({1+i})}^2$=$\frac{(1+3i)(3-i)}{(3+i)(3-i)}+2i$=$\frac{6+8i}{10}+2i$=$\frac{3}{5}+\frac{14}{5}i$,
复数对应点($\frac{3}{5},\frac{14}{5}$)在第一象限.
故选:D.
点评 本题考查复数的代数形式的混合运算,复数的几何意义,是基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
14.设函数f(x)=sin(2x+$\frac{π}{6}$)(x∈[0,$\frac{7π}{6}$]),若方程f(x)=m恰好有三个根,分别为x1,x2,x3(x1<x2<x3),则x1+2x2+x3的值是( )
| A. | $\frac{3π}{4}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{3π}{2}$ |
11.记方程①x2+a1x+1=0,②x2+a2x+1=0,③x2+a3x+1=0,其中a1,a2,a3是正实数,当a1,a2,a3成等比数列,下列选项中,当方程③有实根时,能推出的是( )
| A. | 方程①有实根或方程②无实根 | B. | 方程①有实根或方程②有实根 | ||
| C. | 方程①无实根或方程②无实根 | D. | 方程①无实根或方程②有实根 |
 已知函数g(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$,ω>0)的图象如图所示,函数f(x)=g(x)+$\frac{\sqrt{3}}{2}$cos2x-$\frac{3}{2}$sin2x
已知函数g(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$,ω>0)的图象如图所示,函数f(x)=g(x)+$\frac{\sqrt{3}}{2}$cos2x-$\frac{3}{2}$sin2x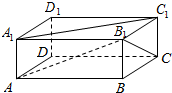 如图所示,ABCD-A1B1C1D1是长方体,AA1=a,∠BAB1=∠B1A1C1=30°,则AB与A1C1所成的角为30°,AA1与B1C所成的角为45°.
如图所示,ABCD-A1B1C1D1是长方体,AA1=a,∠BAB1=∠B1A1C1=30°,则AB与A1C1所成的角为30°,AA1与B1C所成的角为45°. 如图,在△ABC中,BC边上的中线AD长为3,且BD=2,$sinB=\frac{{3\sqrt{6}}}{8}$.
如图,在△ABC中,BC边上的中线AD长为3,且BD=2,$sinB=\frac{{3\sqrt{6}}}{8}$.