题目内容
设点(a,b)是区域
内的随机点,函数y=ax2-4bx+1在区间[1,+∞)上是增函数的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:应用题,概率与统计
分析:作出不等式组对应的平面区域,根据概率的几何概型的概率公式进行计算即可得到结论.
解答:
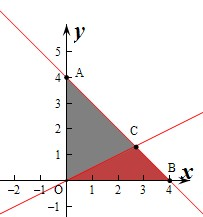 解:作出不等式组
解:作出不等式组
内对应的平面区域如图:对应的图形为△OAB,其中对应面积为S=
×4×4=8,
若f(x)=ax2-4bx+1在区间[1,+∞)上是增函数,
则满足a>0且对称轴x=
≤1,
即
,结合条件
,可得对应的平面区域为△OBC,
由
,
解得a=
,b=
,
∴对应的面积为S1=
×4×
=
,
∴根据几何概型的概率公式可知所求的概率为
=
,
故选:A.
 解:作出不等式组
解:作出不等式组
|
| 1 |
| 2 |
若f(x)=ax2-4bx+1在区间[1,+∞)上是增函数,
则满足a>0且对称轴x=
| 4b |
| 2a |
即
|
|
由
|
解得a=
| 8 |
| 3 |
| 4 |
| 3 |
∴对应的面积为S1=
| 1 |
| 2 |
| 4 |
| 3 |
| 8 |
| 3 |
∴根据几何概型的概率公式可知所求的概率为
| ||
| 8 |
| 1 |
| 3 |
故选:A.
点评:本题主要考查几何概型的概率公式的计算,作出不等式组对应的平面区域是解决本题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
若非空集合 A中的元素具有命题α的性质,集合B中的元素具有命题β的性质,若 A?B,则命题α是命题β的( )条件.
| A、充分非必要 |
| B、必要非充分 |
| C、充分必要 |
| D、既非充分又非必要 |
函数f(x)的定义域为D,若函数f(x)满足:(1)f(x)在D上为单调函数;(2)存在区间[a,b]⊆D,使得f(x)在[a,b]上的值域为[
,
],则称函数f(x)为“取半函数”.若f(x)=logc(cx+t)(c>0,且c≠1)为“取半函数”,则t的取值范围是( )
| a |
| 2 |
| b |
| 2 |
A、(-
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
若条件p:|x|≤2,条件q:x≤a,且p是q的充分不必要条件,则a的取值范围是( )
| A、a≥2 | B、a≤2 |
| C、a≥-2 | D、a≤-2 |
对任意实数k,直线y=kx+1与圆x2+y2=4的位置关系一定是( )
| A、相离 | B、相切 |
| C、相交且不过圆心 | D、相交且过圆心 |
