题目内容
20.已知等差数列{an}满足:a3=3,a5+a7=12,{an}的前n项和为Sn.(1)求an及Sn; (2)令bn=$\frac{1}{{S}_{n}}$(n∈N*),求数列{bn}的前n项和Tn.
分析 (1)利用等差数列的通项公式与求和公式即可得出.
(2)利用“裂项求和”方法即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵a3=3,a5+a7=12,
∴a1+2d=3,2a1+10d=12,
解得a1=d=1.
∴an=1+(n-1)=n,Sn=$\frac{n(n+1)}{2}$.
(2)bn=$\frac{1}{{S}_{n}}$=$2(\frac{1}{n}-\frac{1}{n+1})$,
∴数列{bn}的前n项和Tn=2$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$
=2$(1-\frac{1}{n+1})$
=$\frac{2n}{n+1}$.
点评 本题考查了等差数列的通项公式与求和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据涪陵气象局某日早6点至晚9点在李渡新城区、涪陵老城区两个地区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,李渡新城区、涪陵老城区浓度的方差较小的是( )
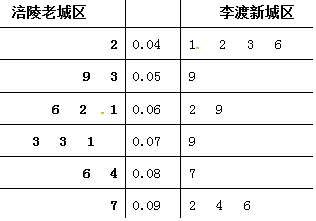

| A. | 李渡新城区 | B. | 涪陵老城区 | ||
| C. | 李渡新城区、涪陵老城区相等 | D. | 无法确定 |
15.已知数列{an}的前n项和Sn=2an-1,则数列{an}的通项公式为( )
| A. | an=2n | B. | an=2n-1 | C. | an=2n-1 | D. | an=2n-1-1 |
5.直线l:x+$\sqrt{3}$y-4=0与圆C:x2+y2=4的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交不过圆心 | D. | 相交且过圆心 |
12.已知log23=a,log25=b,则${log_2}\frac{9}{5}$=( )
| A. | $\frac{2a}{b}$ | B. | 2a-b | C. | a2-b | D. | $\frac{a^2}{b}$ |