题目内容
11.已知数列{log2(an+1)}(n∈N*)为等差数列,且a1=1,a3=7.求:(Ⅰ)数列{an}的通项公式;
(Ⅱ) 数列{an}的前n项和.
分析 (Ⅰ)设等差数列{log2(an+1)}的公差为d.由a1=1,a3=7可求d,由等差数列的通项公式可求log2(an+1),进而可求an;
(Ⅱ)利用(Ⅰ)中的通项公式和分组求和法进行解答即可.
解答 解:(Ⅰ)设等差数列{log2(an+1)}的公差为d.
由a1=1,a3=7得log28=log22+2d,即d=1.
所以log2(an+1)=1+(n-1)×1=n,
即${a_n}+1={2^n}$,
∴${a_n}={2^n}-1$.
(Ⅱ)Sn=a1+a2+a3+…+an=(21-1)+(22-1)+(23-1)+…+(2n-1)=21+22+23+…+2n-n=$\frac{{2(1-{2^n})}}{1-2}-n$=2n+1-2-n.
点评 本题主要考查数列通项公式和前n项和的求解,利用分组求和法是解决本题的关键.

练习册系列答案
相关题目
15.若函数f(x)=ax-lnx在x=$\frac{\sqrt{2}}{2}$处取得极值,则实数a的值为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
13.一个几何体的三视图如图所示,其表面积为6π+$\sqrt{2}$π,则该几何体的体积为( )
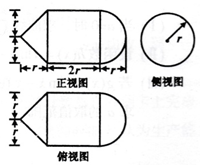

| A. | 4π | B. | 2π | C. | $\frac{11}{3}$π | D. | 3π |
6.设f(x)=$\left\{\begin{array}{l}{lgx,x>0}\\{x{+∫}_{0}^{a}3{t}^{2}dt,x≤0}\end{array}\right.$,若f(f(1))≥1,则实数a的范围是( )
| A. | a≤-1 | B. | a≥-1 | C. | a≤1 | D. | a≥1 |
16.函数f(x)的图象关于y轴对称,且对任意x∈R都有f(x+3)=-f(x),若当x∈($\frac{3}{2}$,$\frac{5}{2}$)时,f(x)=($\frac{1}{2}$)x,则f(2017)=( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -4 | D. | 4 |
1.设全集U={1,2,3,4,5,6,7,8,9},若∁UA={1,3,5,7,9},则集合A=( )
| A. | {2,6,8} | B. | {2,4,6,8} | C. | {0,2,4,6,8} | D. | {0,2,6,8} |