题目内容
已知平面向量
,
,
不共线,且两两之间的夹角都相等,若|
|=2,|
|=2,|
|=1,则
+
+
与
的夹角为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| A、30° | B、60° |
| C、120° | D、150° |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:易得3个向量两两之间的夹角都等于120°,可求
•
=-2,
•
=
•
=-1,代入夹角公式可得.
| a |
| b |
| a |
| c |
| b |
| c |
解答:
解:∵平面向量
,
,
不共线,且两两之间的夹角都相等,
∴这3个向量两两之间的夹角都等于120°,
又∵|
|=2,|
|=2,|
|=1,
∴
•
=2×2×(-
)=-2,
同理可得
•
=
•
=-1,
∴|
+
+
|=
=1
设
+
+
与
的夹角为θ,则 0°≤θ≤180°,
由夹角公式可得cosθ=
=
=
∴θ=60°
故选:B
| a |
| b |
| c |
∴这3个向量两两之间的夹角都等于120°,
又∵|
| a |
| b |
| c |
∴
| a |
| b |
| 1 |
| 2 |
同理可得
| a |
| c |
| b |
| c |
∴|
| a |
| b |
| c |
|
设
| a |
| b |
| c |
| a |
由夹角公式可得cosθ=
(
| ||||||||
|
|
| ||||||||||
| 1×2 |
| 1 |
| 2 |
∴θ=60°
故选:B
点评:本题考查向量的数量积和向量的夹角以及模长公式,解题的关键是正确利用向量的模长公式和求夹角的公式,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式3-|-2x-1|>0的解集是:( )
| A、{x|x<-2或x>1} |
| B、{x|-2<x<1} |
| C、{x|-1<x<2} |
| D、R |
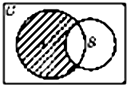 已知全集U=R,集合A={y|y=ln(x2+1),x∈R},集合A={x||x-2|≤1},则如图所示的阴影部分表示的集合为( )
已知全集U=R,集合A={y|y=ln(x2+1),x∈R},集合A={x||x-2|≤1},则如图所示的阴影部分表示的集合为( )| A、{x|0≤x<1或x>3} |
| B、{x|0≤x<1} |
| C、{x|x>3} |
| D、{x|1≤x≤3} |
 已知函数y=6sin(ωx+ϕ)(ω>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若tan∠APB=2,则ω=
已知函数y=6sin(ωx+ϕ)(ω>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若tan∠APB=2,则ω=