题目内容
在△ABC中,A=45°,b=2
,c=1,则a=( )
| 2 |
A、
| ||
| B、5 | ||
C、
| ||
| D、13 |
考点:余弦定理
专题:解三角形
分析:利用余弦定理列出关系式,将b,c,以及cosA的值代入求出a的值即可.
解答:
解:∵在△ABC中,A=45°,b=2
,c=1,
∴由余弦定理得:a2=b2+c2-2bccosA=8+1-4=5,
则a=
.
故选:A.
| 2 |
∴由余弦定理得:a2=b2+c2-2bccosA=8+1-4=5,
则a=
| 5 |
故选:A.
点评:此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
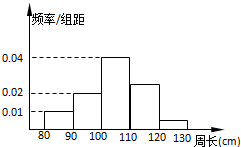 某林业局为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出样本的频率分布直方图(如图),那么估计在这片经济林中,底部周长不小于110cm林木所占百分比为( )
某林业局为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出样本的频率分布直方图(如图),那么估计在这片经济林中,底部周长不小于110cm林木所占百分比为( )| A、70% | B、60% |
| C、40% | D、30% |
以下命题:
(1)z-
是纯虚数
(2)z1+z2∈R?z1=
(3)z1-z2>0?z1>z2
(4)z∈R?z=
(5)z为纯虚数?z+
=0
其中正确命题的个数是( )
(1)z-
. |
| z |
(2)z1+z2∈R?z1=
. |
| z2 |
(3)z1-z2>0?z1>z2
(4)z∈R?z=
. |
| z |
(5)z为纯虚数?z+
. |
| z |
其中正确命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
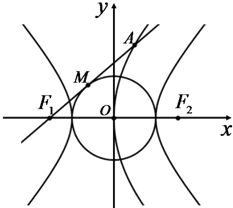 如图,双曲线C1:
如图,双曲线C1:| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
按一定规律排列的数列2,5,11,23,47,x,…中的x应为( )
| A、97 | B、95 | C、93 | D、90 |
在公差为-2的等差数列{an}中,a7是a3与a9的等比中项,Sn为其前n项和,当Sn≥0时n的最大值为( )
| A、10 | B、11 | C、20 | D、21 |
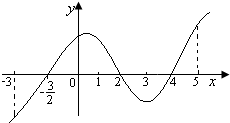 如图是函数y=f(x)的导函数y=f′(x)的图象,对此图象,有如下结论:
如图是函数y=f(x)的导函数y=f′(x)的图象,对此图象,有如下结论: