题目内容
已知正项非常值数列{an}，{bn}满足：an，bn，an+1成等差数列，bn，an+1，bn+1成等比数列．令cn=
，则下列关于数列{cn}的说法正确的是（ ）
| bn |
| A、该数列为等差数列 |
| B、该数列为等比数列 |
| C、该数列的每一项为奇数 |
| D、该数列的每一项为偶数 |
考点：等差数列与等比数列的综合
专题：综合题,等差数列与等比数列
分析：利用等差数列的定义证明数列{cn}为等差数列即可．
解答：
解：∵an，bn，an+1成等差数列，bn，an+1，bn+1成等比数列
∴2bn=an+an+1①，
an+12=bn•bn+1②．
由②得an+1=
③．
将③代入①得，对任意n≥2，n∈N*，
有2bn=
+
．
∵bn＞0，
∴2
=
+
，
∴{
}是等差数列．
即数列{cn}为等差数列．
故选：A．
∴2bn=an+an+1①，
an+12=bn•bn+1②．
由②得an+1=
| bnbn+1 |
将③代入①得，对任意n≥2，n∈N*，
有2bn=
| bn-1bn |
| bnbn+1 |
∵bn＞0，
∴2
| bn |
| bn-1 |
| bn+1 |
∴{
| bn |
即数列{cn}为等差数列．
故选：A．
点评：本题考查了等差、等比数列的通项公式，考查学生分析解决问题的能力，比较基础．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
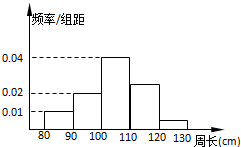某林业局为了解一片经济林的生长情况，随机测量了其中100株树木的底部周长（单位：cm）．根据所得数据画出样本的频率分布直方图（如图），那么估计在这片经济林中，底部周长不小于110cm林木所占百分比为（ ）| A、70% | B、60% |
| C、40% | D、30% |
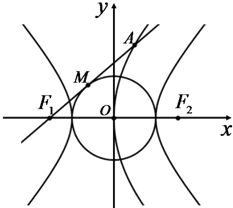如图，双曲线C1：| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不等式（x+1）（x-2）＜0的解集是（ ）
| A、（-∞，-2） |
| B、（-2，1） |
| C、（-∞，-1）∪（2，+∞） |
| D、（-1，2） |
按一定规律排列的数列2，5，11，23，47，x，…中的x应为（ ）
| A、97 | B、95 | C、93 | D、90 |
抛物线y2=8x的焦点与椭圆
+
=1的焦点重合，则椭圆的离心率为（ ）
| x 2 |
| a 2 |
| y 2 |
| 5 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
双曲线x2-
=1的左顶点为A，右焦点为F，则以线段AF为直径的圆被其中一条渐近线截得的弦长为（ ）
| y2 |
| 8 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|