题目内容
不等式x2≥2x的解集是( )
| A、{x|x≥2} |
| B、{x|x≤2} |
| C、{x|0≤x≤2} |
| D、{x|x≤0或x≥2} |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:解方程x2-2x=0,得x1=0,x2=2,由此能求出不等式x2>2x的解集.
解答:
解:∵x2≥2x,
∴x2-2x≥0.
解方程x2-2x=0,得
x1=0,x2=2,
∴不等式x2≥2x的解集是{x|x≤0或x≥2}.
故选:D.
∴x2-2x≥0.
解方程x2-2x=0,得
x1=0,x2=2,
∴不等式x2≥2x的解集是{x|x≤0或x≥2}.
故选:D.
点评:本题考查一元二次不等式的解法,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
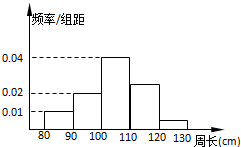 某林业局为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出样本的频率分布直方图(如图),那么估计在这片经济林中,底部周长不小于110cm林木所占百分比为( )
某林业局为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出样本的频率分布直方图(如图),那么估计在这片经济林中,底部周长不小于110cm林木所占百分比为( )| A、70% | B、60% |
| C、40% | D、30% |
用柯西不等式求函数y=
+
+
的最大值为( )
| 2x-3 |
| 2x |
| 7-3x |
A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
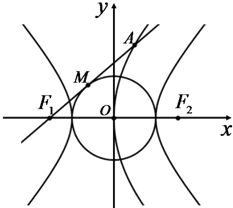 如图,双曲线C1:
如图,双曲线C1:| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不等式(x+1)(x-2)<0的解集是( )
| A、(-∞,-2) |
| B、(-2,1) |
| C、(-∞,-1)∪(2,+∞) |
| D、(-1,2) |
抛物线y2=8x的焦点与椭圆
+
=1的焦点重合,则椭圆的离心率为( )
| x 2 |
| a 2 |
| y 2 |
| 5 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若a1=12,a2=12+22+12,…,an=12+22+…+n2+…+22+12,在运用数学归纳法证明an=
n(2n2+1)时,第二步中从k到k+1应添加的项是( )
| 1 |
| 3 |
| A、k2+1 |
| B、(k2+1)2 |
| C、(k+1)2+k2 |
| D、(k+1)2+2k2 |