题目内容
14.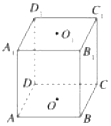 如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.
如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.
分析 DD1与平面AB1C相交;由A1D∥B1C,知A1D∥平面AB1C;A1D1与平面AB1C相交;C1D1与平面AB1C相交;由O1D∥OB1,知O1D∥平面AB1C.
解答 解:在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,
∵DD1∥BB1,BB1∩平面AB1C=B1,
∴DD1与平面AB1C相交;
∵A1D∥B1C,AD1?平面AB1C,B1C?平面AB1C,∴A1D∥平面AB1C;
A1D1∥B1C1,B1C1∩平面AB1C=B1,
∴A1D1与平面AB1C相交;
∵C1D1∥A1B1,A1B1∩平面AB1C=B1,
∴C1D1与平面AB1C相交;
∵O1D∥OB1,OB1?平面AB1C,
∴O1D∥平面AB1C.
∴在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.
故答案为:2.
点评 本题考查直线与平行的位置关系的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
19.设命题 p:?n∈N,3n≥n2+1,则¬p为( )
| A. | ?n∈N,3n<n2+1 | B. | $?{n_0}∈N,{3^{n_0}}<n_0^2+1$ | ||
| C. | ?n∈N,3n≤n2+1 | D. | $?{n_0}∈N,{3^{n_0}}≥n_0^2+1$ |
4.在△ABC中,a、b、c分别为A、B、C所对的边,且2acosB+bcosA=2c,则△ABC是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 斜三角形 |
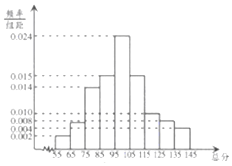 从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.
从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.