题目内容
随机地在棱长为1的正方体ABCD-A1B1C1D1内部取一个点P,满足AP≤1的概率是 .
考点:几何概型
专题:概率与统计
分析:满足AP≤1的轨迹是以A为球心,半径为1的求在正方体内部的部分,利用几何概型的概率公式即可得到结论.
解答:
 解:在正方体ABCD-A1B1C1D1中,与点A距离小于等于1的点在以A为球心,半径为1的八分之一个球内,
解:在正方体ABCD-A1B1C1D1中,与点A距离小于等于1的点在以A为球心,半径为1的八分之一个球内,
其体积为V1=
×
π×13=
;
正方体的体积为13=1,
则点P到点A的距离小于等于1的概率为:
=
,
故答案为:
.
 解:在正方体ABCD-A1B1C1D1中,与点A距离小于等于1的点在以A为球心,半径为1的八分之一个球内,
解:在正方体ABCD-A1B1C1D1中,与点A距离小于等于1的点在以A为球心,半径为1的八分之一个球内,其体积为V1=
| 1 |
| 8 |
| 4 |
| 3 |
| π |
| 6 |
正方体的体积为13=1,
则点P到点A的距离小于等于1的概率为:
| ||
| 1 |
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题考查几何概型的计算,关键在于掌握正方体的结构特征与正方体、球的体积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2014(x)=( )
| A、cosx | B、-cosx |
| C、sinx | D、-sinx |
已知cos(α+
)=
,α∈(-
,0),则tan(2α+
)=( )
| π |
| 3 |
| 4 |
| 5 |
| π |
| 2 |
| 2π |
| 3 |
A、-
| ||
B、
| ||
C、±
| ||
D、
|
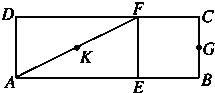 如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为
如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为