题目内容
设a=
(sinx-cosx)dx,则二项式(
-
)8展开式中的常数项是 (用数字作答)
| ∫ | 0 -π |
| x |
| a | ||
|
考点:二项式系数的性质,定积分
专题:二项式定理
分析:利用定积分求出a,在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项.
解答:
解:a=
(sinx-cosx)dx=(-cosx-sinx)
=-1-(1)=-2,
则二项式(
-
)8=(
+
)8的开式的通项公式为Tr+1=
•2r•x4-r,
令4-r=0,求得 r=4,
故二项式(
-
)8展开式中的常数项是
•24=1120,
故答案为:1120.
| ∫ | 0 -π |
| | | 0 -π |
则二项式(
| x |
| a | ||
|
| x |
| 2 | ||
|
| C | r 8 |
令4-r=0,求得 r=4,
故二项式(
| x |
| a | ||
|
| C | 4 8 |
故答案为:1120.
点评:本题主要考查定积分、二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2014(x)=( )
| A、cosx | B、-cosx |
| C、sinx | D、-sinx |
按照如图的程序运行,则输出的K值为( )


| A、2 | B、3 | C、4 | D、5 |
函数y=lg(2-x)的定义域是( )
| A、(-∞,2) |
| B、(-∞,2] |
| C、(2,+∞) |
| D、[2,+∞) |
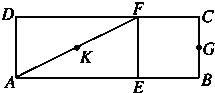 如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为
如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为