题目内容
若某空间几何体的三视图如图所示,则该几何体的体积是( )


| A、32 | B、16 | C、24 | D、48 |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体是四棱锥,根据三视图判断四棱锥的一条侧棱与底面垂直,且高为4,再判断底面四边形的形状及相关几何量的数据,把数据代入棱锥的体积公式计算.
解答:
解:由三视图知:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,高为4,
底面为直角梯形,且直角梯形的高为4,两底边长分别为2、4,
∴几何体的体积V=
×
×4×4=16.
故选:B.
底面为直角梯形,且直角梯形的高为4,两底边长分别为2、4,
∴几何体的体积V=
| 1 |
| 3 |
| 2+4 |
| 2 |
故选:B.
点评:本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所对应的几何量是关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2014(x)=( )
| A、cosx | B、-cosx |
| C、sinx | D、-sinx |
按照如图的程序运行,则输出的K值为( )


| A、2 | B、3 | C、4 | D、5 |
在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是( )
| A、(0,-1,0) |
| B、(0,1,0) |
| C、(1,0,1) |
| D、(0,1,1) |
已知定义在R上的函数f(x)是偶函数,且满足f(1+x)=f(1-x),当x∈[-1,1]时,f(x)=1-x2,若函数g(x)=log5x,则h(x)=f(x)-g(x)在区间(0,5]内的零点的个数是( )
| A、2 | B、3 | C、4 | D、5 |
已知cos(α+
)=
,α∈(-
,0),则tan(2α+
)=( )
| π |
| 3 |
| 4 |
| 5 |
| π |
| 2 |
| 2π |
| 3 |
A、-
| ||
B、
| ||
C、±
| ||
D、
|
函数y=lg(2-x)的定义域是( )
| A、(-∞,2) |
| B、(-∞,2] |
| C、(2,+∞) |
| D、[2,+∞) |
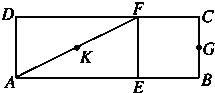 如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为
如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为