题目内容
15. 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,四边形BCDE为矩形,∠PAD=60°,PA=ED=2AE=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,四边形BCDE为矩形,∠PAD=60°,PA=ED=2AE=2.(I)若$\overrightarrow{PF}=λ\overrightarrow{PC}$(λ∈R),且PA∥平面BEF,求λ的值;
(Ⅱ)求证:CB⊥平面PEB.
分析 (I)连接AC交BE于点M,连接FM,由已知得FM∥AP,由EM∥CD,FM∥AP,能求出λ.
(II)先求出$PE=\sqrt{3}$,从而PE⊥AD,进而PE⊥CB,BE⊥CB,由此能证明CB⊥平面PEB.
解答 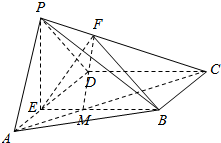 解:(I)连接AC交BE于点M,连接FM,
解:(I)连接AC交BE于点M,连接FM,
因为PA∥平面BEF,平面PAC∩平面BEF=FM,所以FM∥AP.
因为EM∥CD,所以$\frac{AM}{MC}=\frac{AE}{ED}=\frac{1}{2}$
因为FM∥AP,所以$\frac{PF}{FC}=\frac{AM}{MC}=\frac{1}{2}$
所以$λ=\frac{1}{3}$.…(6分)
证明:(II)因为AP=2,AE=1,∠PAD=60°,
所以$PE=\sqrt{3}$,所以PE⊥AD
又平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,PE⊥平面ABCD,
所以PE⊥CB,又BE⊥CB,且PE∩BE=E.
所以CB⊥平面PEB.…(13分)
点评 本题考查实数值的求法,考查线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
3.已知am=-2,则a2m的值为( )
| A. | -4 | B. | 4 | C. | (-2)m | D. | 2m |
20.函数y=($\frac{1}{2}$)x-log2x的零点为x0,则( )
| A. | x0<1 | B. | x0>3 | C. | 2<x0<3 | D. | 1<x0<2 |
5.等比数列{an}中,a3a5=64,则a4=( )
| A. | 8 | B. | -8 | C. | 8或-8 | D. | 16 |