题目内容
4.已知函数f(x)=cosxsin(x+$\frac{π}{3}$)-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{4}$.(1)求f(x)的单调增区间;
(2)求f(x)在区间[0,$\frac{π}{2}$]上的最大值和最小值.
分析 由条件利用三角恒等变换化简函数的解析式,再利用正弦函数的单调性求得函数f(x)的减区间;再根据正弦函数的定义域和值域,求得f(x)在区间[0,$\frac{π}{2}$]上的最大值和最小值.
解答 解:函数f(x)=cosxsin(x+$\frac{π}{3}$)-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{4}$=cosx(sinx•$\frac{1}{2}$+cosx•$\frac{\sqrt{3}}{2}$)-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{4}$
=$\frac{1}{2}$sinxcosx-$\frac{\sqrt{3}}{2}$cos2x+$\frac{\sqrt{3}}{4}$=$\frac{1}{4}$sin2x-$\frac{\sqrt{3}}{2}$•$\frac{1+cos2x}{2}$+$\frac{\sqrt{3}}{4}$=$\frac{1}{2}$sin(2x-$\frac{π}{3}$),
(1)令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{5π}{12}$≤x≤kπ+$\frac{11π}{12}$,
故函数f(x)的减区间为[kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z.
(2)∵x∈[0,$\frac{π}{2}$],∴2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],∴当2x-$\frac{π}{3}$=-$\frac{π}{3}$时,f(x)=$\frac{1}{2}$sin(2x-$\frac{π}{3}$)取得最小值为-$\frac{\sqrt{3}}{4}$,
当2x-$\frac{π}{3}$=$\frac{π}{2}$ 时,f(x)=$\frac{1}{2}$sin(2x-$\frac{π}{3}$)取得最大值为 $\frac{1}{2}$.
点评 本题主要考查三角恒等变换,正弦函数的单调性,正弦函数的定义域和值域,属于中档题.

| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,四边形BCDE为矩形,∠PAD=60°,PA=ED=2AE=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,四边形BCDE为矩形,∠PAD=60°,PA=ED=2AE=2.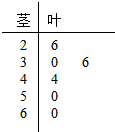 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值.即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米--75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区今年9月每天的PM2.5监测数据中,按系统抽样方法抽取了某6天的数据作为样本,其监测值如茎叶图所示.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值.即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米--75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区今年9月每天的PM2.5监测数据中,按系统抽样方法抽取了某6天的数据作为样本,其监测值如茎叶图所示.