题目内容
设等差数列{an}的前n项和公式是Sn=n2-21n，
（1）求它的通项公式an
（2）求Sn的最小值．
（1）求它的通项公式an
（2）求Sn的最小值．
考点：等差数列的性质
专题：等差数列与等比数列
分析：（1）根据等差数列的性质，求出首项和公差，即可求它的通项公式an
（2）根据二次函数的性质即可求Sn的最小值．
（2）根据二次函数的性质即可求Sn的最小值．
解答：
解：（1）∵等差数列{an}的前n项和公式是Sn=n2-21n，
∴当n=1时，a1=1-21=-20，
当n≥2时，an=Sn-Sn-1=2n-22，
则通项公式an=2n-22．
（2）∵Sn=n2-21n=(n-
)2-
，
∴当n=10或n=11时，（Sn）min=-110．
∴当n=1时，a1=1-21=-20，
当n≥2时，an=Sn-Sn-1=2n-22，
则通项公式an=2n-22．
（2）∵Sn=n2-21n=(n-
| 21 |
| 2 |
| 441 |
| 4 |
∴当n=10或n=11时，（Sn）min=-110．
点评：本题主要考查等差数列的通项公式的计算，根据等差数列的定义是解决本题的关键，比较基础．
练习册系列答案
小学课时特训系列答案
相关题目
若函数f（x）在给定区间M上存在正数t，使得对于任意的x∈M，有x+t∈M，且f（x+t）≥f（x），则称f（x）为M上t级类增函数，则下列命题中正确的是（ ）
A、函数f（x）=
| ||||||
| B、函数f（x）=|log2（x-1）|是（1，+∞）上的1级类增函数 | ||||||
C、若函数f（x）=sinx+ax为[
| ||||||
| D、若函数f（x）=x2-3x为[1，+∞）上的t级类增函数，则实数t的取值范围为[2，+∞） |
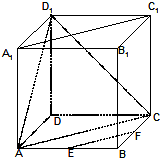如图，棱长为2的正方体ABCD-A1B1C1D1中，点E，F分别为棱AB，BC的中点．