题目内容
现有10名教师,其中男教师6名,女教师4名.
(1)要从中选2名教师去参加会议,有多少种不同的选法?
(2)现要从中选出4名教师去参加会议,求男、女教师各选2名的概率.
(1)要从中选2名教师去参加会议,有多少种不同的选法?
(2)现要从中选出4名教师去参加会议,求男、女教师各选2名的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)从10名教师中选2名去参加会议的选法数为
,进而由组合数公式,可得答案.
(2)先计算从10名教师中选4名的选法总数,再计算男、女教师各选2名的选法总数,代入古典概型概率计算公式,可得答案.
| C | 2 10 |
(2)先计算从10名教师中选4名的选法总数,再计算男、女教师各选2名的选法总数,代入古典概型概率计算公式,可得答案.
解答:
解:(1)从10名教师中选2名去参加会议的选法数,
就是从10个不同元素中取出2个元素的组合数,即
=
=45(种).…(5分)
(2)从10名教师中选4名共有
=
=210种 …(7分)
从6名男教师中选2名的选法有
种,从4名女教师中选2名的选法有
种,根据分步乘法计数原理,
共有选法
•
=
•
=90(种).…(9分)
所以男、女教师各选2名的概率P=
=
…(11分)
答:男、女教师各选2名的概率是
.…(12分)
就是从10个不同元素中取出2个元素的组合数,即
| C | 2 10 |
| 10×9 |
| 2×1 |
(2)从10名教师中选4名共有
| C | 4 10 |
| 10×9×8×7 |
| 4×3×2×1 |
从6名男教师中选2名的选法有
| C | 2 6 |
| C | 2 4 |
共有选法
| C | 2 6 |
| C | 2 4 |
| 6×5 |
| 2×1 |
| 4×3 |
| 2×1 |
所以男、女教师各选2名的概率P=
| 90 |
| 210 |
| 3 |
| 7 |
答:男、女教师各选2名的概率是
| 3 |
| 7 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
已知函数f(x)=
x3-x2+ax+b,其中a<0,如果存在实数t,使f′(t)<0,则f′(2-t)•f′(
)的值( )
| 1 |
| 3 |
| 3t+1 |
| 4 |
| A、必为正数 | B、必为负数 |
| C、必为非负 | D、必为非正 |
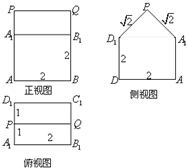 某一几何体的三视图如图所示.按照给出的尺寸(单位:cm):
某一几何体的三视图如图所示.按照给出的尺寸(单位:cm):