题目内容
已知函数f(x)=
x3-x2+ax+b,其中a<0,如果存在实数t,使f′(t)<0,则f′(2-t)•f′(
)的值( )
| 1 |
| 3 |
| 3t+1 |
| 4 |
| A、必为正数 | B、必为负数 |
| C、必为非负 | D、必为非正 |
考点:导数的运算
专题:函数的性质及应用,导数的概念及应用
分析:求函数的导数,则f′(x)为开口向上的抛物线,根据二次函数的图象和性质判断f′(2-t)与f′(
)的符号即可得到结论.
| 3t+1 |
| 4 |
解答:
解:∵f(x)=
x3-x2+ax+b,
∴使f′(x)=x2-2x+a=(x-1)2+(a-1),
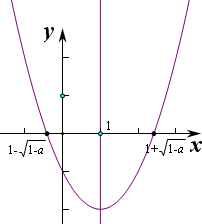
二次函数的对称轴为x=1,顶点为(1,a-1),开口向上的抛物线,
若f'(t)<0,所以a<1,
而对称轴与x轴的交点分别为:(1-
,0)和 (1+
,0),两交点的水平距离为2.
通过观察f'(x)图象可知:
∵f'(t)<0,
∴t范围为∈(1-
,1+
)
∵1-
<t<1+
,
∴-1-
<-t<-1+
,1-
<2-t<1+
,
此时f′(2-t)<0.
∵1-
<t<1+
,
∴3-3
<3t<3+3
,4-3
<3t+1<4+3
,
则
<
<
,
即1-
<
<1+
,
则(1-
,1+
)?∈(1-
,1+
),
∴f′(
)<0,
即f′(2-t)•f′(
)>0.
故选:A
| 1 |
| 3 |
∴使f′(x)=x2-2x+a=(x-1)2+(a-1),
二次函数的对称轴为x=1,顶点为(1,a-1),开口向上的抛物线,
若f'(t)<0,所以a<1,
而对称轴与x轴的交点分别为:(1-
| 1-a |
| 1-a |
通过观察f'(x)图象可知:
∵f'(t)<0,
∴t范围为∈(1-
| 1-a |
| 1-a |
∵1-
| 1-a |
| 1-a |
∴-1-
| 1-a |
| 1-a |
| 1-a |
| 1-a |
此时f′(2-t)<0.
∵1-
| 1-a |
| 1-a |

∴3-3
| 1-a |
| 1-a |
| 1-a |
| 1-a |
则
4-3
| ||
| 4 |
| 3t+1 |
| 4 |
4+3
| ||
| 4 |
即1-
3
| ||
| 4 |
| 3t+1 |
| 4 |
3
| ||
| 4 |
则(1-
3
| ||
| 4 |
3
| ||
| 4 |
| 1-a |
| 1-a |
∴f′(
| 3t+1 |
| 4 |
即f′(2-t)•f′(
| 3t+1 |
| 4 |
故选:A
点评:本题主要考查导数的计算,以及二次函数的图象和性质,考查学生的推理能力.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
若复数z2+2=0,则z3等于( )
A、±2
| ||
| B、2 | ||
C、±2
| ||
D、-2
|
一位母亲纪录了儿子3到9岁的身高数据(略),她根据这些数据建立的身高y(cm)与年龄x的回归模型为
=7.19x+73.93,用此模型预测孩子10岁时的身高,则有( )
 |
| y |
| A、身高一定是145.83cm |
| B、身高在145.83cm左右 |
| C、身高在145.83cm以上 |
| D、身高在145.83cm以下 |
设f(x)是奇函数,且在(0,+∞)内是增函数,又f(-2)=0,则x•f(x)<0的解集是( )
| A、{x|x<-2或0<x<2} |
| B、{x|-2<x<0或x>2} |
| C、{x|x<-2或x>2} |
| D、{x|-2<x<0或0<x<2} |
已知函数y=cos(x-
)的图象为C,为了得到函数y=cos(x+
)的图象只需把C上所有的点( )
| 2π |
| 9 |
| 2π |
| 9 |
A、向右平行移动
| ||
B、向左平行移动
| ||
C、向右平行移动
| ||
D、向左平行移动
|
正方体ABCD-A1B1C1D1中,O为侧面BCC1B1的中心,则AO与平面ABCD所成的角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
平面向量
,
中,若
=(4,-3),|
|=1,且
•
=5,则向量
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
A、(
| ||||
B、(-
| ||||
C、(
| ||||
D、(-
|