题目内容
已知定义在R上的函数f(x)=x|x-a|,下列说法中,描述完全正确的个数为( )
①无论a取何实数,函数f(x)的图象均过原点;
②当a>2时,函数f(x)在区间(-∞,2]上的解析式为f(x)=-x2+ax;
③当a=1时,函数f(x)有最大值
;
④当a=2时,若函数y=f(x)-m有3个不同的零点,则0<m<1.
①无论a取何实数,函数f(x)的图象均过原点;
②当a>2时,函数f(x)在区间(-∞,2]上的解析式为f(x)=-x2+ax;
③当a=1时,函数f(x)有最大值
| 1 |
| 4 |
④当a=2时,若函数y=f(x)-m有3个不同的零点,则0<m<1.
| A、0 | B、1 | C、2 | D、3 |
考点:函数的图象
专题:函数的性质及应用
分析:代入特殊点验证①,比较a与x的大小可去掉绝对值符号来判断②,
考虑函数的单调性可判断③,化为分段函数画函数的图象可判断④.
考虑函数的单调性可判断③,化为分段函数画函数的图象可判断④.
解答:
解:①、∵f(0)=0×|0-a|=0,故函数f(x)的图象过原点,正确;
②、∵x∈(-∞,2]上,∴x<2,而a>2时,∴x<a,因此函数f(x)=x(a-x)=-x2+ax,正确;
③、当a=1时,函数f(x)=x|x-1|,当x>1时,f(x)=x(x-1)=x2-x在区间(1,+∞)递增,无最大值,错误;
④、当a=1时,函数f(x)=x|x-2|=
,图象如下图:
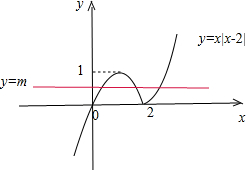
当0<m<1时,函数y=m与函数y=x|x-2|有3个交点,则函数y=f(x)-m有3个不同的零点,所以④正确.
综上①②④正确,
故选:D.
②、∵x∈(-∞,2]上,∴x<2,而a>2时,∴x<a,因此函数f(x)=x(a-x)=-x2+ax,正确;
③、当a=1时,函数f(x)=x|x-1|,当x>1时,f(x)=x(x-1)=x2-x在区间(1,+∞)递增,无最大值,错误;
④、当a=1时,函数f(x)=x|x-2|=
|

当0<m<1时,函数y=m与函数y=x|x-2|有3个交点,则函数y=f(x)-m有3个不同的零点,所以④正确.
综上①②④正确,
故选:D.
点评:本题考查函数的单调性及函数零点的判断,同时考查分段函数的性质,注意,带有绝对值符号的函数常化为分段函数.

练习册系列答案
相关题目
已知 p:“一个有理数与一个无理数的和是无理数”,q:“一个有理数与一个无理数的积是无理数”,则命题 p、q、p∧q中的真命题是( )
| A、p | B、q |
| C、p∧q | D、p、q、p∧q |
若等比数列{an}的前n项和Sn=2n+r,则r=( )
| A、2 | B、1 | C、0 | D、-1 |
已知幂函数f(x)满足f(
)=4,则f(x)的图象所分布的象限是( )
| 1 |
| 2 |
| A、第一、二象限 |
| B、第一、三象限 |
| C、第一、四象限 |
| D、只在第一象限 |
双曲线
-
=1的一个焦点到一条渐近线的距离为( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、6 | B、5 | C、4 | D、3 |
若复数z满足(3+4i)z=4-3i,则z的虚部为( )
| A、1 | B、i | C、-1 | D、-i |