题目内容
双曲线
-
=1的一个焦点到一条渐近线的距离为( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、6 | B、5 | C、4 | D、3 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据双曲线方程即可求出右焦点坐标,渐近线方程,而根据点到直线的距离公式即可求得焦点到渐近线的距离.
解答:
解:双曲线
-
=1的右焦点为(5,0),渐近线方程为y=±
x;
∴(5,0)到y=±
的距离为:
=4.
故选C.
| x2 |
| 9 |
| y2 |
| 16 |
| 4 |
| 3 |
∴(5,0)到y=±
| 4 |
| 3 |
| ||||
|
故选C.
点评:考查双曲线的标准方程,双曲线的焦点,以及渐近线方程的概念及求法,点到直线的距离公式.

练习册系列答案
相关题目
函数f(x)=|ex+
|(a∈R)在区间[0,1]上单调递增,则a的取值范围是( )
| a |
| ex |
| A、a∈[-1,1] | ||
| B、a∈[-1,0] | ||
| C、a∈[0,1] | ||
D、a∈[-
|
若非直角△ABC的内角A、B、C成等差数列,则tanA+tanC-tanAtanBtanC=( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
设偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是减函数,则f(-2),f(π),f(-1)的大小关系是( )
| A、f(-2)<f(-1)<f(π) |
| B、f(-2)<f(π)<f(-1) |
| C、f(-2)>f(π)>f(-1) |
| D、f(-1)>f(-2)>f(π) |
函数f(x)=
的定义域是( )
| 7+x |
| A、[-7,+∞) |
| B、(-∞,-7] |
| C、[0,+∞) |
| D、R |
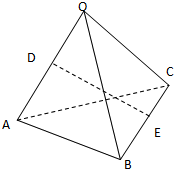 如图,空间四边形OABC各边以及AC,BO的长都是1,点D是边OA,BC的中点,连接DE.
如图,空间四边形OABC各边以及AC,BO的长都是1,点D是边OA,BC的中点,连接DE.