题目内容
| C | 1 33 |
| C | 2 33 |
| C | 3 33 |
| C | 33 33 |
| A、0 | B、11 | C、2 | D、7 |
考点:二项式系数的性质
专题:二项式定理
分析:直接利用二项式定理系数的性质求出表达式的值,然后利用二项式定理求解即可.
解答:
解:
+
+
+…+
=233-1=811-1=(9-1)11-1,因为(9-1)11的展开式的最后一项是-1,其余的项都能被9整除,
所以
+
+
+…+
除以9的余数是:7.
故选:D.
| C | 1 33 |
| C | 2 33 |
| C | 3 33 |
| C | 33 33 |
所以
| C | 1 33 |
| C | 2 33 |
| C | 3 33 |
| C | 33 33 |
故选:D.
点评:本题考查二项式定理的应用,二项式定理系数的性质,考查转化思想以及计算能力.

练习册系列答案
相关题目
递减的等差数列{an}的前n项和Sn满足S5=S10,则欲使Sn取最大值,n的值为( )
| A、10 | B、7 | C、9 | D、7或8 |
计算
cosxdx的结果是( )
| ∫ |
-
|
| A、4 | B、2 | C、0 | D、π |
设复数z满足iz=1,其中i为虚数单位,则z等于( )
| A、-i | B、i | C、-1 | D、1 |
(理科)已知-3<a<2,3<b<4,则
的取值范围为( )
| a |
| b |
A、(-1,
| ||||
B、(-
| ||||
C、(-1,
| ||||
D、(-
|
已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,f(x)递减,都有f(x)≥0,则a=f(2010),b=f(
),c=-f(
)的大小关系是( )
| 5 |
| 4 |
| 1 |
| 2 |
| A、b<c<a |
| B、c<b<a |
| C、a<c<b |
| D、a<b<c |
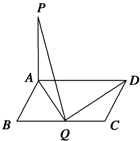 如图所示,已知矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥QD,则a=( )
如图所示,已知矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥QD,则a=( )