题目内容
15.成等差数列的三个正数的和等于15,并且这三个数分别加上2,5,13后成为等比数列{bn}中的b3,b4,b5.数列{bn}的前n项和为Sn,求证:数列{Sn+$\frac{5}{4}$}是等比数列.分析 设成等差数列的三个正数分别为a-d,a,a+d,则a-d+a+a+d=15,解得a=5.根据这三个数分别加上2,5,13后成为等比数列{bn}中的b3,b4,b5.可得(5+5)2=(5-d+2)(5+d+13),解得:d=2.可得b1与公比q.l利用求和公式可得Sn,即可证明.
解答 证明:设成等差数列的三个正数分别为a-d,a,a+d,则a-d+a+a+d=15,解得a=5.
∵这三个数分别加上2,5,13后成为等比数列{bn}中的b3,b4,b5.
∴(5+5)2=(5-d+2)(5+d+13),解得:d=-13(舍去),或2.
∴d=2时,b3=5,b4=10,b5=20.可得公比q=$\frac{10}{5}$=2.
${b}_{1}×{2}^{2}$=5,解得b1=$\frac{5}{4}$.
∴Sn=$\frac{\frac{5}{4}({2}^{n}-1)}{2-1}$=5×2n-2-$\frac{5}{4}$,
∴Sn+$\frac{5}{4}$=5×2n-2,
∴数列{Sn+$\frac{5}{4}$}是等比数列,公比为2,首项为$\frac{5}{2}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
20.若a=sin147°,b=cos55°,c=tan215°,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | b<a<c |
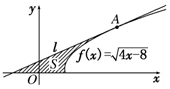 如图,过点A(6,4)作曲线f(x)=$\sqrt{4x-8}$的切线l.
如图,过点A(6,4)作曲线f(x)=$\sqrt{4x-8}$的切线l.