题目内容
已知x,y∈N*,且1+2+…+y=1+9+92+…+9x-1,则将y表示成x的函数,其解析式是y= .
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由已知条件,利用等差数列和等比数列的前n项和,能求出函数的解析式.
解答:
解:∵1+2+…+y=1+9+92+…+9x-1,
∴
(1+y)=
,
即
(y+1)=
,
整理,得(2y+1)2=9x,
∵x,y∈N*,
∴2y+1=3x,
解得y=
.
故答案为:
.
∴
| y |
| 2 |
| 1×(1-9x) |
| 1-9 |
即
| y |
| 2 |
| 9x-1 |
| 8 |
整理,得(2y+1)2=9x,
∵x,y∈N*,
∴2y+1=3x,
解得y=
| 3x-1 |
| 2 |
故答案为:
| 3x-1 |
| 2 |
点评:本题考查函数的解析式的求法,是基础题,解题时要注意等差数列和等比数列的前n项和的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
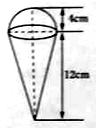 如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了并流入杯中,会溢出杯子吗?请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π≈3.14)
如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了并流入杯中,会溢出杯子吗?请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π≈3.14)
