题目内容
已知函数f(x)=
(a为常数),x=2是函数f(x)的一个极值点.
(Ⅰ)求实数a的值;
(Ⅱ)如果当x≥2时,不等式f(x)≥
恒成立,求实数m的最大值;
(Ⅲ)求证:n-2(
+
+
+…+
)<ln(n+1)
| 1+ln(x-1) |
| x-a |
(Ⅰ)求实数a的值;
(Ⅱ)如果当x≥2时,不等式f(x)≥
| m |
| x |
(Ⅲ)求证:n-2(
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n |
| n+1 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由题意得:f(x)=
,由x=2是函数f(x)的一个极值点,得f′(2)=0,解得:a=1,
(Ⅱ)由(Ⅰ)得f(x)=
,定义域为(1,+∞),得问题等价于m≤x•
在[2,+∞)上恒成立,构造函数g(x)=x•
,则g′(x)=
,令h(x)=x-1-ln(x-1),则h′(x)=
,得h(x)≥h(2)=1>0,从而g(x)在[2,+∞)递增,进而求出m的范围.
(Ⅲ)由(Ⅱ)得:x≥2时,f(x)≥
,即
≥
,令x-1=
,得n-2(
+
+…+
)<ln(
×
×…×
),即n-2(
+
+…+
)<ln(n+1).
| ||
| (x-a)2 |
(Ⅱ)由(Ⅰ)得f(x)=
| 1+ln(x-1) |
| x-1 |
| 1+ln(x-1) |
| x-1 |
| 1+ln(x-1) |
| x-1 |
| x-1-ln(x-1) |
| (x-1)2 |
| x-2 |
| x-1 |
(Ⅲ)由(Ⅱ)得:x≥2时,f(x)≥
| 2 |
| x |
| 1+ln(x-1) |
| x-1 |
| 2 |
| x |
| k+1 |
| k |
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
解答:
解:(Ⅰ)由题意得:f(x)=
,
∵x=2是函数f(x)的一个极值点,
∴f′(2)=0,解得:a=1,
(Ⅱ)由(Ⅰ)得f(x)=
,定义域为(1,+∞),
∴问题等价于m≤x•
在[2,+∞)上恒成立,
构造函数g(x)=x•
,则g′(x)=
,
令h(x)=x-1-ln(x-1),则h′(x)=
,
∴x≥2时,h′(x)>0,h(x)在[2,+∞)递增,
∴h(x)≥h(2)=1>0,
∴g′x)>0,
∴g(x)在[2,+∞)递增,
∴g(x)min=g(2)=2,∴m≤2,
∴实数m的最大值为2;
(Ⅲ)由(Ⅱ)得:x≥2时,f(x)≥
,即
≥
,
整理得ln(x-1)≥1-
>1-
,
令x-1=
,则1-
=1-2
,
即ln
>1-2
,
k=1时,1-2×
<ln
,
k=2时,1-2×
<ln
,
…,
k=n时,1-2
<ln
,
将以上不等式两端分别相加得:
n-2(
+
+…+
)<ln(
×
×…×
),
即n-2(
+
+…+
)<ln(n+1).
| ||
| (x-a)2 |
∵x=2是函数f(x)的一个极值点,
∴f′(2)=0,解得:a=1,
(Ⅱ)由(Ⅰ)得f(x)=
| 1+ln(x-1) |
| x-1 |
∴问题等价于m≤x•
| 1+ln(x-1) |
| x-1 |
构造函数g(x)=x•
| 1+ln(x-1) |
| x-1 |
| x-1-ln(x-1) |
| (x-1)2 |
令h(x)=x-1-ln(x-1),则h′(x)=
| x-2 |
| x-1 |
∴x≥2时,h′(x)>0,h(x)在[2,+∞)递增,
∴h(x)≥h(2)=1>0,
∴g′x)>0,
∴g(x)在[2,+∞)递增,
∴g(x)min=g(2)=2,∴m≤2,
∴实数m的最大值为2;
(Ⅲ)由(Ⅱ)得:x≥2时,f(x)≥
| 2 |
| x |
| 1+ln(x-1) |
| x-1 |
| 2 |
| x |
整理得ln(x-1)≥1-
| 2 |
| x |
| 2 |
| x-1 |
令x-1=
| k+1 |
| k |
| 2 |
| x-1 |
| k |
| k+1 |
即ln
| k+1 |
| k |
| k |
| k+1 |
k=1时,1-2×
| 1 |
| 2 |
| 2 |
| 1 |
k=2时,1-2×
| 2 |
| 3 |
| 3 |
| 2 |
…,
k=n时,1-2
| n |
| n+1 |
| n+1 |
| n |
将以上不等式两端分别相加得:
n-2(
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
即n-2(
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
点评:本题考察了函数的单调性,求函数的最值问题,求参数的范围问题,关于导数的应用,是一道综合题.

练习册系列答案
相关题目
 某英语学习小组共12名同学进行英语听力测试,随机抽取6名同学的测试成绩(单位:分),用茎叶图记录如下,其中茎为十位数,叶为个位数.
某英语学习小组共12名同学进行英语听力测试,随机抽取6名同学的测试成绩(单位:分),用茎叶图记录如下,其中茎为十位数,叶为个位数.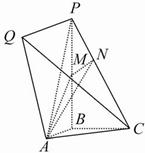 如图所示的几何体中,PB⊥平面ABC,PQ∥AB,PQ=PB=1,AB=BC=
如图所示的几何体中,PB⊥平面ABC,PQ∥AB,PQ=PB=1,AB=BC= 如图,圆的割线ABC经过⊙O圆心,AD为圆的切线,D为切点,作CE⊥AD,交AD延长线于E,若AB=2,AD=4,则CE的长为
如图,圆的割线ABC经过⊙O圆心,AD为圆的切线,D为切点,作CE⊥AD,交AD延长线于E,若AB=2,AD=4,则CE的长为