题目内容

若在（1+ax）5的展开式中x3的系数为-80，求a的值．
考点：二项式系数的性质
专题：二项式定理
分析：先求出二项式展开式的通项公式，再令x的幂指数等于3，求得r的值，即可求得展开式中x3的系数，再根据x3的系数为-80，求得a的值．
解答： 解：∵（1+ax）5的展开式的通项公式为 Tr+1=
C
r
5
•ar•xr，令r=3，
可得展开式中x3的系数为
C
3
5
•a3=-80，求得a=-2．
点评：本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于基础题．
练习册系列答案
相关题目
已知集合M={x|-1＜x≤1}，N={x|1≤2x＜4}，则M∩N（　　）
A、{x|-1＜x＜1}
B、{x|0≤x＜1}
C、{x|0≤x≤1}
D、{x|-1＜x＜2}
计算：
（1）（C
 
2
100
+C
 
97
100
）÷A
 
3
101
；                      
（2）C
 
3
3
+C
 
3
4
+…+C
 
3
10
．
（3）
C
m
n+1
C
m
n
-
C
n-m+1
n
C
n-m
n
．
某英语学习小组共12名同学进行英语听力测试，随机抽取6名同学的测试成绩（单位：分），用茎叶图记录如下，其中茎为十位数，叶为个位数．
（1）根据茎叶图计算样本均值；
（2）成绩高于样本均值的同学为优秀，根据茎叶图估计该小组12名同学中有几名优秀同学；
（3）从该小组12名同学中任取2人，求仅有1人是来自随机抽取6人中优秀同学的概率．
在平面直角坐标系xOy中，设圆x2+y2=1在矩阵A=
10
02
对应的变换作用下得到曲线F，求曲线F的方程．
某牛奶厂2008年初有资金1000万元，由于引进了先进设备，资金年平均增长率可达到50%．每年年底扣除下一年的消费基金x万元后，剩余资金投入再生产．
（1）分别写出这家牛奶厂2009年初和2010年初投入再生产的剩余资金的表达式．
（2）预计2012年底，这家牛奶厂将转向经营，需资金2000万元（该年底不再扣除下年的消费基金），当消费基金x不超过多少万元时，才能实现转向经营的目标（精确到万元）？
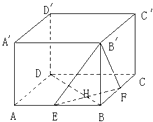在棱长为a的正方体ABCD-A′B′C′D′中，如图E、F分别为棱AB与BC的中点，EF∩BD=H；
（Ⅰ）求二面角B′-EF-B的正切值；
（Ⅱ）试在棱B′B上找一点M，使D′M⊥面EFB′，并证明你的结论．
射击比赛中，每位射手射击队10次，每次一发，击中目标得3分，未击中目标得0分，每射击一次，凡参赛者加2分，已知小李击中目标的概率为0.8．
（1）设X为小李击中目标的次数，求X的概率分布；
（2）求小李在比赛中的得分的数学期望与方差．
某工厂生产甲、乙两种产品，已知生产甲种产品1吨需耗A种矿石8吨、B种矿石8吨、煤5吨；生产乙种产品1吨需耗A种矿石4吨、B种矿石8吨、煤10吨．每1吨甲种产品的利润是500元，每1吨乙种产品的利润是400元．工厂在生产这两种产品的计划中要求消耗A种矿石不超过320吨、B种矿石不超过400吨、煤不超过450吨．甲、乙两种产品应各生产多少吨能使利润总额达到最大？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网