题目内容
解下列不等式并将结果用集合的形式表示.
(1)-x2-2x+3>0;
(2)
≥1.
(1)-x2-2x+3>0;
(2)
| 2x-1 |
| x+1 |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:(1))-x2-2x+3>0化为x2+2x-3<0,l利用一元二次不等式的解法即可得出;
(2)
≥1化为
≥0?
,解出即可.
(2)
| 2x-1 |
| x+1 |
| x-2 |
| x+1 |
|
解答:
解:(1))-x2-2x+3>0化为x2+2x-3<0,解得-3<x<1,
∴不等式的解集为(-3,1);
(2)
≥1化为
≥0?
,
解得x≥2或x<-1.
∴不等式的解集为{x|x≥2或x<-1|}.
∴不等式的解集为(-3,1);
(2)
| 2x-1 |
| x+1 |
| x-2 |
| x+1 |
|
解得x≥2或x<-1.
∴不等式的解集为{x|x≥2或x<-1|}.
点评:本题考查了一元二次不等式的解法、分式不等式的等价转化方法,考查了计算能力,属于基础题.

练习册系列答案
相关题目
 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=3,DE=4.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=3,DE=4.
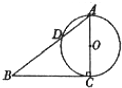 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,求 BD的长.
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,求 BD的长.