题目内容

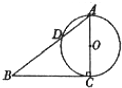如图，已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径的圆与AB交于点D，求 BD的长．
考点：相似三角形的判定
专题：立体几何
分析：由AC是⊙O的直径，AC⊥BC，可得BC是⊙O的切线．利用切割线定理可得：BC2=BD•BA即可得出．
解答： 解：AB=
AC2+BC2
=5．
∵AC是⊙O的直径，AC⊥BC，∴BC是⊙O的切线．
∴BC2=BD•BA，
∴BD=
BC2
BA
=
42
5
=
16
5
．
点评：本题考查了圆的切线的判定、勾股定理、切割线定理，属于基础题．
练习册系列答案
相关题目
已知矩阵M=
2a
2b
的两个特征值分别为λ1=-1和λ2=4．
（1）求实数a，b的值；
（2）求直线x-2y-3=0在矩阵M所对应的线性变换作用下的象的方程．
设函数f（x）=12x-x3+b．
（1）当b=1时，求函数在区间[-3，3]上的最小值；
（2）若函数y=f（x）有三个不同的零点，求b的取值范围．
直线l：y=x-1与抛物线C：y2=2px（p＞0）相交于A，B两点，且l过C的焦点．
（1）求抛物线C的方程；
（2）若以AB为直径作圆Q，求圆Q的方程．
解下列不等式并将结果用集合的形式表示．
（1）-x2-2x+3＞0；
（2）
2x-1
x+1
≥1．
已知函数f（x）=lnx+ax-1，a∈R
（Ⅰ）求f（x）在x=1处的切线方程；
（Ⅱ）若不等式f（x）≤0恒成立，求a的取值范围．
已知函数f（x）=ax-3，g（x）=bx-1+cx-2（a，b∈R）且g（-
1
2
）-g（1）=f（0）．
（1）试求b，c所满足的关系式；
（2）若b=0，试讨论方程f（x）+x|x-a|g（x）=0零点的情况．
已知点P的极坐标是（1，
π
4
），则过点P且垂直极轴的直线极坐标方程是
 
．
五个人站成一排照相，其中甲与乙不相邻，且甲与丙也不相邻的不同站法有
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网