题目内容
6.设A={x|2≤x≤6},B={x|2a≤x≤a+3},若A∪B=A,则实数a的取值范围是( )| A. | [1,3] | B. | [3,+∞) | C. | [1,+∞) | D. | (1,3) |
分析 由已知得B?A,根据B=∅和B≠∅两种情况分类讨论经,能求出实数a的取值范围.
解答 解:∵A={x|2≤x≤6},B={x|2a≤x≤a+3},A∪B=A,
∴B?A,
当B=∅时,2a>a+3,解得a>3;
当B≠∅时,$\left\{\begin{array}{l}{2a≥2}\\{a+3≤6}\end{array}\right.$,解得1≤a≤3.
综上,a≥1.
∴实数a的取值范围是[1,+∞).
故选:C.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意并集性质的合理运用.

练习册系列答案
相关题目
5.复数z满足$z=\frac{1+i}{i}(i$是虚数单位),则|z|=( )
| A. | l | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
6.以下函数在R上为减函数的是( )
| A. | y=log${\;}_{\frac{1}{2}}$x | B. | y=x-1 | C. | y=($\frac{1}{2}$)x | D. | y=x2 |

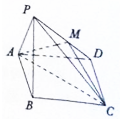 如图,已知四棱锥P-ABCD,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.