题目内容
1.设函数f(x)是定义在R上的偶函数,且对于任意的x都有f(x)=f(x+2),当x∈[0,1]时,f(x)=x+1,则f($\frac{3}{2}$)=$\frac{3}{2}$.分析 根据函数的奇偶性得到f(x)在[-1,0]的解析式,得到f($\frac{3}{2}$)=f(-$\frac{1}{2}$),求出函数值即可.
解答 解:函数f(x)是定义在R上的偶函数,
当x∈[0,1]时,f(x)=x+1,
故x∈[-1,0)时,f(x)=-x+1,
故f($\frac{3}{2}$)=f($\frac{3}{2}$-2)=f(-$\frac{1}{2}$)=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$
点评 本题考查了求函数的解析式问题,考查函数的奇偶性和周期性问题,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知数列{an}满足${a_1}=2,{a_{n+1}}=\frac{{{a_n}-1}}{{{a_n}+1}}(n∈N*)$,则该数列的前2017项的乘积a1a2a3…a2017=( )
| A. | 2 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -2 |
6.设A={x|2≤x≤6},B={x|2a≤x≤a+3},若A∪B=A,则实数a的取值范围是( )
| A. | [1,3] | B. | [3,+∞) | C. | [1,+∞) | D. | (1,3) |
13.已知定义在R上的奇函数f(x)和偶函数g(x)满足:f(x)+g(x)=ex,则( )
| A. | $f(x)=\frac{{{e^x}+{e^{-x}}}}{2}$ | B. | $f(x)=\frac{{{e^x}-{e^{-x}}}}{2}$ | C. | $g(x)=\frac{{{e^x}-{e^{-x}}}}{2}$ | D. | $g(x)=\frac{{{e^{-x}}-{e^x}}}{2}$ |
11.已知α,β为锐角,且cosα=$\frac{3}{5}$,sin(α-β)=$\frac{5}{13}$,则cosβ=( )
| A. | -$\frac{16}{65}$ | B. | $\frac{56}{65}$ | C. | $\frac{16}{65}$ | D. | -$\frac{56}{65}$ |
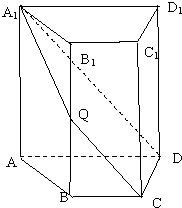 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为梯形,AD∥BC,AD=2BC,过 A1,C,D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为梯形,AD∥BC,AD=2BC,过 A1,C,D三点的平面记为α,BB1与α的交点为Q.