题目内容
已知集合M={1，
，b}，N={0，a+b，b2}，M=N，求a1+b1+a2+b2+…+an+bn．
| a |
| b |
考点：集合的相等
专题：集合
分析：根据集合相等，确定a，b的值即可得到结论．
解答：
解：∵集合M={1，
，b}，N={0，a+b，b2}，M=N，
∴b≠0，则
=0，即a=0，
此时M={1，0，b}，N={0，b，b2}，
则b2=1，解得b=1或-1，
当b=1时，M={1，0，1}不成立，
当b=-1，={1，0，-1}，N={0，-1，1}，满足条件，
故a=0，b=-1，
则a1+b1+a2+b2+…．+an+bn=b1+b2+…．+bn=（-1）+（-1）2+（-1）3+…+（-1）n
当n为奇数时原式=-1．当n为偶数时原式=0
| a |
| b |
∴b≠0，则
| a |
| b |
此时M={1，0，b}，N={0，b，b2}，
则b2=1，解得b=1或-1，
当b=1时，M={1，0，1}不成立，
当b=-1，={1，0，-1}，N={0，-1，1}，满足条件，
故a=0，b=-1，
则a1+b1+a2+b2+…．+an+bn=b1+b2+…．+bn=（-1）+（-1）2+（-1）3+…+（-1）n
当n为奇数时原式=-1．当n为偶数时原式=0
点评：本题主要考查集合相等的应用，根据集合相等确定元素关系是解决本题的关键．
练习册系列答案
相关题目
所有棱长均为1的四棱柱ABCD-A1B1C1C1如图所示，∠DAB=60°，CC1⊥A1C1．
已知椭圆C：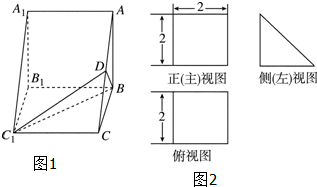
直三棱柱ABC-A1B1C1的直观图（图1）及三视图（图2）如图所示，D为AC的中点
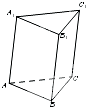如图，在三棱柱ABC-A1B1C1中，侧棱AA1与侧面BCC1B1的距离为2，侧面BCC1B1的面积为4，此三棱柱ABC-A1B1C1的体积为