题目内容
3.已知复数$z=\frac{a+i}{2-i}$(i 为虚数单位)的共轭复数在复平面内对应的点在第三象限,则实数a的取值范围是( )| A. | $({-2,\frac{1}{2}})$ | B. | $({-\frac{1}{2},2})$ | C. | (-∞,-2) | D. | $({\frac{1}{2},+∞})$ |
分析 利用复数的运算法则、共轭复数的定义、几何意义即可得出.
解答 解:复数$z=\frac{a+i}{2-i}$=$\frac{(a+i)(2+i)}{(2-i)(2+i)}$=$\frac{2a-1}{5}$+$\frac{(2+a)}{5}$i的共轭复数$\frac{2a-1}{5}$-$\frac{(2+a)}{5}$i的共在复平面内对应的点在第三象限,
∴$\frac{2a-1}{5}$<0,-$\frac{(2+a)}{5}$<0,
解得a$<\frac{1}{2}$,且a>-2,
则实数a的取值范围是$(-2,\frac{1}{2})$.
故选:A.
点评 本题考查了复数的运算法则、共轭复数的定义、几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
14.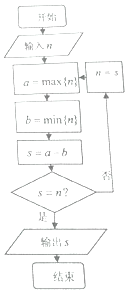 正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )
正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )
 正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )
正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )| A. | 6174 | B. | 7083 | C. | 8341 | D. | 8352 |
11.在平行四边形ABCD中,点M,N分别在边BC,CD上,且满足BC=3MC,DC=4NC,若AB=4,AD=3,则$\overrightarrow{AN}•\overrightarrow{MN}$=( )
| A. | $-\sqrt{7}$ | B. | 0 | C. | $\sqrt{7}$ | D. | 7 |
8.已知函数 f ( x) 的部分图象如图所示,则 f ( x) 的解析式可以是( )
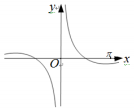

| A. | f(x)=$\frac{{2-{x^2}}}{2x}$ | B. | f(x)=$\frac{cosx}{x^2}$ | C. | f(x)=$\frac{{{{cos}^2}x}}{x}$ | D. | f(x)=$\frac{cosx}{x}$ |
12.平行四边形ABCD的两条对角线相交于点M,点P是线段BD上任意一点.若$|\overrightarrow{AB}|=2,|\overrightarrow{AD}|=1$,且∠BAD=60°,则$\overrightarrow{AP}•\overrightarrow{CP}$的取值范围是( )
| A. | $[1,\frac{7}{4}]$ | B. | $[-\frac{7}{4},-1]$ | C. | $[-\sqrt{2},-1]$ | D. | $[-1,\sqrt{2}]$ |
13.等比数列中{an},a1,a5为方程x2-10x+16=0的两根,则a3=( )
| A. | 4 | B. | 5 | C. | ±4 | D. | ±5 |
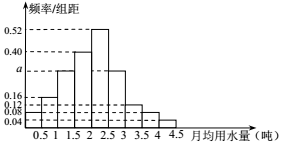 我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.