题目内容
12.平行四边形ABCD的两条对角线相交于点M,点P是线段BD上任意一点.若$|\overrightarrow{AB}|=2,|\overrightarrow{AD}|=1$,且∠BAD=60°,则$\overrightarrow{AP}•\overrightarrow{CP}$的取值范围是( )| A. | $[1,\frac{7}{4}]$ | B. | $[-\frac{7}{4},-1]$ | C. | $[-\sqrt{2},-1]$ | D. | $[-1,\sqrt{2}]$ |
分析 通过图形,分别表示则$\overrightarrow{AP}$,$\overrightarrow{CP}$,然后进行向量数量积的运算即可.
解答 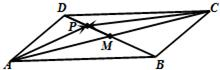 解:设$\overrightarrow{BP}$=λ$\overrightarrow{BD}$,λ∈[0,1],由题意可得
解:设$\overrightarrow{BP}$=λ$\overrightarrow{BD}$,λ∈[0,1],由题意可得
$\overrightarrow{AP}•\overrightarrow{CP}$=($\overrightarrow{AB}$+λ$\overrightarrow{BD}$)•($\overrightarrow{CB}$+λ$\overrightarrow{BD}$)
=($\overrightarrow{AB}$+λ$\overrightarrow{BD}$)•(-$\overrightarrow{AD}$+λ$\overrightarrow{BD}$)
=[$\overrightarrow{AB}$+λ($\overrightarrow{AD}$-$\overrightarrow{AB}$)]•[-$\overrightarrow{AD}$+λ($\overrightarrow{AD}$-$\overrightarrow{AB}$)]
=[(1-λ)$\overrightarrow{AB}$+λ$\overrightarrow{AD}$]•[(-λ$\overrightarrow{AB}$)+(λ-1)$\overrightarrow{AD}$]
=λ•(λ-1)${\overrightarrow{AB}}^{2}$+(-2λ2+2λ-1)$\overrightarrow{AB}•\overrightarrow{AD}$+λ(λ-1)${\overrightarrow{AD}}^{2}$
=4λ•(λ-1)+(-2λ2+2λ-1)•2•1•cos60°+λ(λ-1)•1
=3λ2-3λ-1=3${(λ-\frac{1}{2})}^{2}$-$\frac{7}{4}$,
故当λ=$\frac{1}{2}$时,$\overrightarrow{AP}•\overrightarrow{CP}$ 取得最小值为-$\frac{7}{4}$,
当λ=0或1时,$\overrightarrow{AP}•\overrightarrow{CP}$ 取得最大值-1,
故$\overrightarrow{AP}•\overrightarrow{CP}$ 的范围为[-$\frac{7}{4}$,-1],
故选:B.
点评 本题考查平面向量的数量积的运算,用已知向量表示未知向量,是中档题.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | $({-2,\frac{1}{2}})$ | B. | $({-\frac{1}{2},2})$ | C. | (-∞,-2) | D. | $({\frac{1}{2},+∞})$ |
女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |

(Ⅱ)分别求女性用户评分的众数,男性用户评分的中位数;
(Ⅲ)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列2×2列联表,并回答是否有95%的把握认为性别和对手机的“认可”有关;
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P(K2≥x0) | 0.05 | 0.01 |
| x0 | 3.841 | 6.635 |
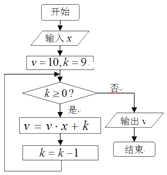 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出的v值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出的v值为( )| A. | 9×210-2 | B. | 9×210+2 | C. | 9×211+2 | D. | 9×211-2 |
| A. | $\frac{1}{2}$ | B. | -1 | C. | -$\frac{3}{2}$ | D. | -2 |