题目内容
13．等比数列中{an}，a1，a5为方程x2-10x+16=0的两根，则a3=（ ）| A． | 4 | B． | 5 | C． | ±4 | D． | ±5 |
分析 由题意和韦达定理得：a1+a5=10，a1a5=16，判断出a1，a5为正数，由等比数列的性质和项的符号求出a3的值．
解答 解：∵a1，a5为方程x2-10x+16=0的两根，
∴a1+a5=10，a1a5=16，则a1，a5为正数，
在等比数列中{an}中，a32=a1a5=16，则a3=±4，
∵a1，a5为正数，∴a3=4，
故选：A．
点评 本题考查等比数列的性质和项的符号，以及韦达定理的应用，属于基础题．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
3．已知复数$z=\frac{a+i}{2-i}$（i 为虚数单位）的共轭复数在复平面内对应的点在第三象限，则实数a的取值范围是（ ）
| A． | $（{-2，\frac{1}{2}}）$ | B． | $（{-\frac{1}{2}，2}）$ | C． | （-∞，-2） | D． | $（{\frac{1}{2}，+∞}）$ |
1．
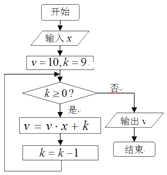秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入x的值为2，则输出的v值为（ ）
秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入x的值为2，则输出的v值为（ ）| A． | 9×210-2 | B． | 9×210+2 | C． | 9×211+2 | D． | 9×211-2 |
8．已知全集U=R，集合$A=\left\{{x|{2^x}＞\frac{1}{2}}\right\}，B=\left\{{x|{{log}_3}x＜1}\right\}$，则A∩（∁UB）=（ ）
| A． | （-1，+∞） | B． | [3，+∞） | C． | （-1，0）∪（3，+∞） | D． | （-1，0]∪[3，+∞） |
18．已知△ABC中，$AC=2，AB=2\sqrt{7}，cos∠BAC=\frac{{2\sqrt{7}}}{7}$且D是BC的中点，则中线AD的长为（ ）
| A． | 2 | B． | 4 | C． | $2\sqrt{3}$ | D． | $4\sqrt{3}$ |
5．i为虚数单位，复数$\frac{3+i}{1-i}$的虚部是（ ）
| A． | 2i | B． | 2 | C． | -2i | D． | -1 |
2．对于实数m＞-3，若函数$y={（\frac{1}{2}）^x}$图象上存在点（x，y）满足约束条件$\left\{\begin{array}{l}x-y+3≥0\\ x+2y+3≥0\\ x≤m\end{array}\right.$，则实数m 的最小值为（ ）
| A． | $\frac{1}{2}$ | B． | -1 | C． | -$\frac{3}{2}$ | D． | -2 |
3．设x，y满足约束条件$\left\{\begin{array}{l}{x≥y}\\{y≥4x-3}\\{x≥0，y≥0}\end{array}\right.$，若目标函数2z=2x+ny（n＞0），z的最大值为2，则y=tan（nx+$\frac{π}{6}$）的图象向右平移$\frac{π}{6}$后的表达式为（ ）
| A． | y=tan（2x+$\frac{π}{6}$） | B． | y=tan（x-$\frac{π}{6}$） | C． | y=tan（2x-$\frac{π}{6}$） | D． | y=tan2x |